题目内容
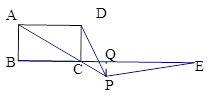
已知四边形ABCD,点E是射线BC上的一个动点(点E不与B、C两点重合),线段BE的垂直平分线交射线AC于点P,联结DP,PE.

(1)若四边形ABCD是正方形,猜想PD与PE的关系,并证明你的结论.
(2)若四边形ABCD是矩形,(1)中的PD与PE的关系还成立吗? (填:成立或不成立).

(3)若四边形ABCD是矩形,AB=6,cos∠ACD=![]() ,设AP=x,△PCE的面积为y,当AP>
,设AP=x,△PCE的面积为y,当AP>![]() AC时,求y与x之间的函数关系式.
AC时,求y与x之间的函数关系式.
(1)见解析
(2)成立
(3)见解析
解析:(1)PE=PD,……………………………..(1分)
PE⊥PD ……………………………..(2分)
① 点E在射线BC边上,且交点P在对角线AC上时,连结PB
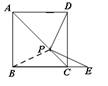
∵四边形ABCD是正方形,
∴AB=AD,∠BAP=∠DAP。
又∵AP=AP,∴△BAP≌△DAP(SAS)。
∴PB=PD
∵点P在BE的垂直平分线上
∴PB=PE
∴PE=PD
∵△BAP≌△DAP,∴∠DPA=∠APB.
又∵∠APB=180°-45°-∠ABP=135°-∠ABP,
∴∠DPA=135°-∠ABP。
又∵PE=PB,∴∠BPE=180°-2∠PBE
∴∠DPE=360°-∠DPA-∠APB—∠BPE=360°-2(135°-∠ABP)
-180°+2∠PBE =360°-270°+2∠ABP-180°+2∠PBE=90°
∴PE⊥PD ………………………..(3分)
② P、C两点重合
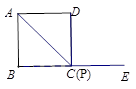
![]() ………………………..(4分)
………………………..(4分)
③ 当点E在BC边的延长线上且点P在对角
线AC的延长线上时,连结PB
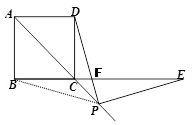
同理可证∴△BAP≌△DAP(SAS)。
∴ PB=PD
∴∠PBA=∠PDA
∴∠PBE=∠PDC
∵点P在BE的垂直平分线上
∴PB=PE
∴∠PBE=∠PEB
∴∠PDC=∠PEB
∴∠DFC=∠EFP
∴∠EPF =∠DCF=90°
∴PE⊥PD …………………………………………..(5分)
结论成立
(3)(1)中的猜想不成立. …………………………..(6分)
(4) ①当点P在线段AC上时
∵四边形ABCD是矩形,AB=6
∴DC=AB=6
![]() ∴∠ABC=∠ADC=90°
∴∠ABC=∠ADC=90°
∵cos∠ACD=
∴AD=8,AC=10
作PQ⊥BC于点Q
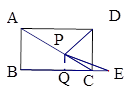
∴PQ∥AB
∴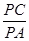 =
=![]()
∴ =
=![]()
∴BQ=![]() x, ∴BE=
x, ∴BE=![]() x,∴CE=
x,∴CE=![]() x-8
x-8
∴△CPQ∽△CAB
∴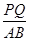 =
=![]() ∴
∴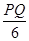 =
=![]()
∴PQ=6-![]() x
x
∴y=![]() EC×PQ
EC×PQ
=(![]() x-8)( 6-
x-8)( 6-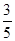 x)
x)
=-![]() x2+
x2+![]() x-24(5<x<10) ……………………………..(7分)
x-24(5<x<10) ……………………………..(7分)
②当点P在线段AC的延长线上时
∵PQ∥AB
∴△CPQ∽△CAB
∴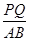 =
=![]()
∴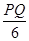 =
=![]()
∴PQ=![]() x-6
x-6
∴ =
=![]()
∴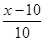 =
=![]()
∴CQ=![]() x-8
x-8
∴BQ=![]() x
x
∴BE=![]() x
x
∴EC=![]() x-8
x-8
∴y =![]() EC×PQ
EC×PQ
=![]() (
(![]() x-8) (
x-8) ( x-6)
x-6)
= ![]()
![]() -
-![]() x+24(x>10) ………………………………………..(8分)
x+24(x>10) ………………………………………..(8分)
[注]学生正确答案与本答案不同,请老师们酌情给分。

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案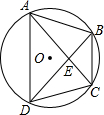 如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3.下列命题错误的是( )
如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3.下列命题错误的是( )| A、△ABE≌△DCE | B、∠BDA=45° | C、S四边形ABCD=24.5 | D、图中全等的三角形共有2对 |

A、
| ||
B、
| ||
C、
| ||
D、
|
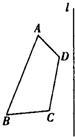 32、如图,已知四边形ABCD和直线L.
32、如图,已知四边形ABCD和直线L.