题目内容
一次函数y=（m+2）x+m的图象过第一、三、四象限．
（1）求m的取值范围；
（2）若m为整数，求函数y=mx2-mx的对称轴与顶点坐标．
解：（1）∵y=（m+2）x+m过第一、三、四象限，
∴
，
∴
，
∴-2＜m＜0；
（2）取m=-1代入y=mx2-mx得y=-x2+x=-（x-
）2+
，
则对称轴为：
，顶点坐标为
．
分析：（1）根据二次函数的性质以及图象与系数的关系可得出m+2与m的符号，进而得出m的取值范围即可；
（2）可以去m=-1，利用配方法求出其顶点坐标和对称轴即可．
点评：此题主要考查了二次函数的性质以及利用配方法求二次函数的顶点坐标等知识，根据函数所在象限得出m的取值范围是解题关键．
∴
，∴
，∴-2＜m＜0；
（2）取m=-1代入y=mx2-mx得y=-x2+x=-（x-
）2+，则对称轴为：
，顶点坐标为．分析：（1）根据二次函数的性质以及图象与系数的关系可得出m+2与m的符号，进而得出m的取值范围即可；
（2）可以去m=-1，利用配方法求出其顶点坐标和对称轴即可．
点评：此题主要考查了二次函数的性质以及利用配方法求二次函数的顶点坐标等知识，根据函数所在象限得出m的取值范围是解题关键．
练习册系列答案
相关题目
为保护学生视力，课桌椅的高度都是按一定的关系配套设计的，研究表明：假设课桌的高度为ycm，椅子的高度为xcm，则y应是x的一次函数，下表列出两套符合条件的课桌椅的高度：第一套第二套椅子高度xcm桌子高度ycm．
（1）请确定y与x的函数关系式．
（2）现有一把高39cm的椅子和一张高为78.2的课桌，它们是否配套？为什么？
| 第一套 | 第二套 | |
| 椅子高度xcm | 40 | 37 |
| 桌子高度ycm | 75 | 70 |
（2）现有一把高39cm的椅子和一张高为78.2的课桌，它们是否配套？为什么？
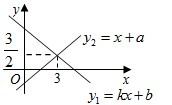一次函数y1=kx+b与y2=x+a的图象如图，下列结论中：