题目内容
在不透明的口袋中装有质地、外观完全相同的分别刻有数字为0，2，4的三个小球，从中任意摸出两个小球，将这两个小球上的数字分别作为a、b的值，则使关于x、y的二元一次方程组
只有正整数解的概率为________．
0
分析：根据题意利用树状图列举出所有等可能的结果，把得出的每一个结果中a与b的值代入方程组中求出解，找出解为正整数的结果数目，两者的比值即为所求的概率．
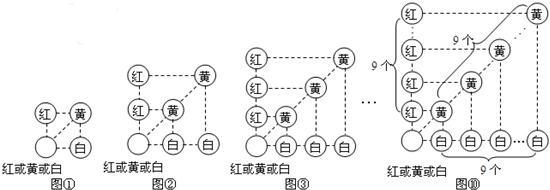
解答：根据题意画树状图如下：
根据图形得到所有等可能的结果为：（0，2），（0，4），（2，0），（2，4），（4，0），（4，2）共6种，
当a=0，b=2时，代入方程组得：
，解得
；
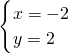当a=0，b=4时，代入方程组得：
，解得：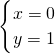
；
当a=2，b=0时，代入方程组得：
，解得：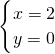
；
当a=2，b=4时，代入方程组得：
，只要满足x+2y=2即可（无数解）；
当a=4，b=0时，代入方程组得：
，解得：
；
当a=4，b=2时，代入方程组得：
，解得：
，
能使二元一次方程组解为正整数的结果有0个，
则P（方程组解为正整数）=0．
故答案为：0．
点评：此题考查了利用树状图求事件发生的概率，利用树状图可以将复杂的概率问题化繁为简，化难为易，这种方法可以直观的把所有可能的结果一一罗列出来，方便于计算，本题的关键是让学生理解同时摸两个球，其实质是摸一个球不放回再摸一球，同时注意把得出的所有可能的a与b的值代入方程组，求出方程组的解进行判断，得到满足题意的结果，从而求出事件发生的概率．
分析：根据题意利用树状图列举出所有等可能的结果，把得出的每一个结果中a与b的值代入方程组中求出解，找出解为正整数的结果数目，两者的比值即为所求的概率．
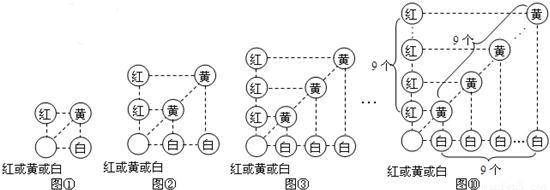
解答：根据题意画树状图如下：
根据图形得到所有等可能的结果为：（0，2），（0，4），（2，0），（2，4），（4，0），（4，2）共6种，
当a=0，b=2时，代入方程组得：
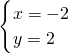，解得；当a=0，b=4时，代入方程组得：
，解得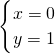：；当a=2，b=0时，代入方程组得：
，解得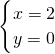：；当a=2，b=4时，代入方程组得：
，只要满足x+2y=2即可（无数解）；当a=4，b=0时，代入方程组得：
，解得：；当a=4，b=2时，代入方程组得：
，解得：，能使二元一次方程组解为正整数的结果有0个，
则P（方程组解为正整数）=0．
故答案为：0．
点评：此题考查了利用树状图求事件发生的概率，利用树状图可以将复杂的概率问题化繁为简，化难为易，这种方法可以直观的把所有可能的结果一一罗列出来，方便于计算，本题的关键是让学生理解同时摸两个球，其实质是摸一个球不放回再摸一球，同时注意把得出的所有可能的a与b的值代入方程组，求出方程组的解进行判断，得到满足题意的结果，从而求出事件发生的概率．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
下列说法中正确的是（ ）
| A、抛掷质地均匀的硬币100次，必然有50次正面朝上 | B、在不透明的口袋中装有1只红球、5只白球（除颜色外其余都相同）搅匀后从中任意摸出一个球，摸出的一定是白球 | C、抛掷一枚质地均匀的骰子，朝上的点数为奇数与朝上的点数为偶数的概率相等 | D、某种福利彩票中奖的概率是1%，买100张该种彩票一定能中奖 |
