题目内容
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且 ![]() =
= ![]() =
= ![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D. 
(1)求证:CD是⊙O的切线;
(2)若CD=2 ![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】
(1)证明:连结OC,如图,
∵ ![]() =
= ![]() ,
,
∴∠FAC=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠FAC=∠OCA,
∴OC∥AF,
∵CD⊥AF,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:连结BC,如图,
∵AB为直径,
∴∠ACB=90°,
∵ ![]() =
= ![]() =
= ![]() ,
,
∴∠BOC= ![]() ×180°=60°,
×180°=60°,
∴∠BAC=30°,
∴∠DAC=30°,
在Rt△ADC中,CD=2 ![]() ,
,
∴AC=2CD=4 ![]() ,
,
在Rt△ACB中,BC= ![]() AC=
AC= ![]() ×4
×4 ![]() =4,
=4,
∴AB=2BC=8,
∴⊙O的半径为4.
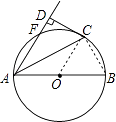
【解析】(1)连结OC,由 ![]() =
= ![]() ,根据圆周角定理得∠FAC=∠BAC,而∠OAC=∠OCA,则∠FAC=∠OCA,可判断OC∥AF,由于CD⊥AF,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;(2)连结BC,由AB为直径得∠ACB=90°,由
,根据圆周角定理得∠FAC=∠BAC,而∠OAC=∠OCA,则∠FAC=∠OCA,可判断OC∥AF,由于CD⊥AF,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;(2)连结BC,由AB为直径得∠ACB=90°,由 ![]() =
= ![]() =
= ![]() 得∠BOC=60°,则∠BAC=30°,所以∠DAC=30°,在Rt△ADC中,利用含30度的直角三角形三边的关系得AC=2CD=4
得∠BOC=60°,则∠BAC=30°,所以∠DAC=30°,在Rt△ADC中,利用含30度的直角三角形三边的关系得AC=2CD=4 ![]() ,在Rt△ACB中,利用含30度的直角三角形三边的关系得BC=
,在Rt△ACB中,利用含30度的直角三角形三边的关系得BC= ![]() AC=4,AB=2BC=8,所以⊙O的半径为4.
AC=4,AB=2BC=8,所以⊙O的半径为4.
【考点精析】解答此题的关键在于理解三角形三边关系的相关知识,掌握三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边,以及对切线的判定定理的理解,了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.

 备战中考寒假系列答案
备战中考寒假系列答案