题目内容
 如图,点A在双曲线
如图,点A在双曲线 上,点B在双曲线
上,点B在双曲线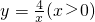 上,且AB∥y轴,点P是y轴上的任意一点,则(1)AB=______; (2)△PAB的面积为______.
上,且AB∥y轴,点P是y轴上的任意一点,则(1)AB=______; (2)△PAB的面积为______.
解:延长BA交x轴于C点,连结OA、OB,如图,
∵点A在双曲线 上,点B在双曲线
上,点B在双曲线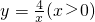 上,
上,
∴S△OAC= ×2=1,S△OBC=
×2=1,S△OBC= ×4=2,
×4=2,
∴S△OAB=2-1=1,
∵AB∥y轴,
∴S△PAB=S△OAB=1.
若A点的横坐标为x,则 •x•AB=1,AB=
•x•AB=1,AB= .
.
故答案为 ;1.
;1.
分析:延长BA交x轴于C点,连结OA、OB,根据k的几何意义得到S△OAC= ×2=1,S△OBC=
×2=1,S△OBC= ×4=2,可计算出S△OAB=1,由AB∥y轴得到S△PAB=S△OAB=1,若A点的横坐标为x,则
×4=2,可计算出S△OAB=1,由AB∥y轴得到S△PAB=S△OAB=1,若A点的横坐标为x,则 •x•AB=1,AB=
•x•AB=1,AB= .
.
点评:本题考查了反比例函数y=kx(k≠0)系数k的几何意义:从反比例函数y=kx(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.

∵点A在双曲线
 上,点B在双曲线
上,点B在双曲线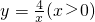 上,
上,∴S△OAC=
 ×2=1,S△OBC=
×2=1,S△OBC= ×4=2,
×4=2,∴S△OAB=2-1=1,
∵AB∥y轴,
∴S△PAB=S△OAB=1.
若A点的横坐标为x,则
 •x•AB=1,AB=
•x•AB=1,AB= .
.故答案为
 ;1.
;1.分析:延长BA交x轴于C点,连结OA、OB,根据k的几何意义得到S△OAC=
 ×2=1,S△OBC=
×2=1,S△OBC= ×4=2,可计算出S△OAB=1,由AB∥y轴得到S△PAB=S△OAB=1,若A点的横坐标为x,则
×4=2,可计算出S△OAB=1,由AB∥y轴得到S△PAB=S△OAB=1,若A点的横坐标为x,则 •x•AB=1,AB=
•x•AB=1,AB= .
.点评:本题考查了反比例函数y=kx(k≠0)系数k的几何意义:从反比例函数y=kx(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•江阴市模拟)如图,点A在双曲线上,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当OA=4时,△ABC周长为
(2013•江阴市模拟)如图,点A在双曲线上,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当OA=4时,△ABC周长为
 轴,垂足为
轴,垂足为 轴交于点F,已知AC:
轴交于点F,已知AC: 上,且OA=4,过A作AC⊥
上,且OA=4,过A作AC⊥ 轴,垂足为C,OA的垂直平分线交OC于B,则△ABC的周长为 ( )
轴,垂足为C,OA的垂直平分线交OC于B,则△ABC的周长为 ( ) 
 B.5 C.
B.5 C. D.
D.
 上,AB⊥x轴于B,且△AOB的面积S△AOB=2,则k=______.
上,AB⊥x轴于B,且△AOB的面积S△AOB=2,则k=______.