Question

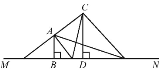
【题目】如图,AB⊥MN,CD⊥MN,垂足分别为B,D,AB=2,CD=4,BD=3.若在直线MN上存在点P,能使△PAB与△PCD相似,则PB=_____

Answer 1

【答案】3或1或

【解析】

分三种情形①延长CA交MN于P1，此时△P1AB∽△P1CD．②当点P2在BD上时．③当点P3在BD的延长线时．分别列出方程即可即可．

如图，

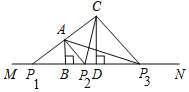
①延长CA交MN于P1，

∵AB⊥MN，CD⊥MN，

∴AB∥CD

∴△P1AB∽△P1CD，

∴，

∴P1B=BD=3．

②当点P2在BD上时，设P2B=x，若△ABP2∽△CDP2则有，

∴，

∴x=1，

∴P2B=1，

若△ABP2∽△P2DC，则有，方程无解．

③当点P3在BD的延长线时，∵△P3AB∽△CP3D，

∴，

∴，

∴x=或（舍弃）

∴P3B=，

综上所述，满足条件的PB的长为3或1或．