Question

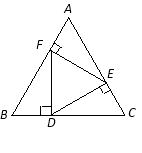
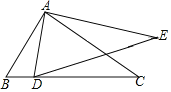
【题目】如图，在Rt△ABC中，∠BAC＝90°，AB＝3，BC＝5，点D是线段BC上一动点，连接AD，以AD为边作△ADE，使△ADE∽△ABC，则△ADE的最小面积与最大面积之比等于_____．

Answer 1

【答案】

【解析】

根据勾股定理得到AC＝4，当AD⊥BC时，△ADE的面积最小，根据三角形的面积 公式得到AD＝，根据相似三角形的性质得到AE＝，当D与C重合时，△ADE的面积最大，根据相似三角形的性质得到AE＝，根据三角形的面积公式即可得到结论．

解：∵在Rt△ABC中，∠BAC＝90°，AB＝3，BC＝5，

∴AC＝4，

当AD⊥BC时，△ADE的面积最小，

∴AD＝，

∵△ADE∽△ABC，

∴，

∴，

∴AE＝，

∴△ADE的最小面积；

当D与C重合时，△ADE的面积最大，

∵△ADE∽△ABC，

，

，

∴AE＝，

∴△ADE的最大面积＝，

∴△ADE的最小面积与最大面积之比＝，

故答案为： ．