题目内容
【题目】我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.

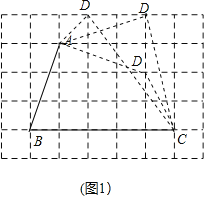
(1)已知:如图1,四边形ABCD的顶点A,B,C在网格格点上,请你在如下的5![]() 7的网格中画出3个不同形状的等邻边四边形ABCD,要求顶点D在网格格点上;
7的网格中画出3个不同形状的等邻边四边形ABCD,要求顶点D在网格格点上;
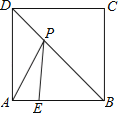
(2)如图2,矩形ABCD中,AB=![]() ,BC=5,点E在BC边上,连结DE画AF
,BC=5,点E在BC边上,连结DE画AF![]() DE于点F,若DE=
DE于点F,若DE=![]() CD,找出图中的等邻边四边形;
CD,找出图中的等邻边四边形;
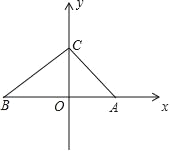
(3)如图3,在Rt![]() ABC中,
ABC中,![]() ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,求BM的长.
ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,求BM的长.
【答案】(1)见解析;(2)四边形ABEF和四边形ABED都是等邻边四边形;(3)当BM为2或3或![]() 时,四边形ACDM是“等邻边四边形”.
时,四边形ACDM是“等邻边四边形”.
【解析】
(1)根据”等邻边四边形”的定义画出3个不同形状的等邻边四边形;
(2)根据题意求出DE,根据勾股定理求出CE,计算得到BE=AB,根据等邻边四边形的定义判断即可;
(3)分AM=AC、DM=DC、MA=MD三种情况,根据勾股定理、等腰三角形的性质计算即可.
(1)3个不同形状的等邻边四边形ABCD如图所示:
(2)四边形ABEF和四边形ABED都是等邻边四边形,
∵四边形ABCD是矩形,
∴AD=BC=5,CD=AB=![]() ,
,
∴DE=![]() CD=
CD=![]() ,
,
由勾股定理得,CE=![]() =
=![]() ,
,
∴BE=BC-CE=5-![]() =
=![]() ,
,
∴BE=AB,
∴四边形ABEF和四边形ABED都是等邻边四边形;
(3)①当AM=AC时,BM=2;
②当DM=DC时,如图3,作DH⊥AB于H,

∵∠ACB=90°,AB=4,AC=2,
∴BC=![]() ,∠B=30°,
,∠B=30°,
∴BD=DM=![]() ,
,
在Rt△BDH中,BH=BD×cosB=![]() ,
,
∵DM=DB,DH⊥AB,
∴BM=2BH=3;
③当MA=MD时,如图4,作DH⊥AB于H,

设MA=MD=x,
由②得,BH=![]() ,DH=
,DH=![]() ,
,
则MH=4-x-![]() =
=![]() -x,
-x,
在Rt△MDH中,DM2=MH2+DH2,即x2=(![]() -x)2+(
-x)2+(![]() )2,
)2,
解得,x=![]() ,即AM=
,即AM=![]() ,
,
∴BM=4-![]() =
=![]() ,
,
综上所述,当BM为2或3或![]() 时,四边形ACDM是“等邻边四边形”.
时,四边形ACDM是“等邻边四边形”.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案【题目】学校为了解全校![]() 名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
频道 | 新闻 | 体育 | 电影 | 科教 | 其他 |
人数 |
|
|
|
|
|
![]() 求调查的学生人数及统计图表中
求调查的学生人数及统计图表中![]() 的值;
的值;
![]() 求选择其他频道在统计图中对应扇形的圆心角的度数;
求选择其他频道在统计图中对应扇形的圆心角的度数;
![]() 求全校最爱选择电影频道的学生人数.
求全校最爱选择电影频道的学生人数.