题目内容
销售甲、乙两种商品所得利润分别为y1(万元)和y2(万元),它们与投入资金u的关系式为y1= ,y2=
,y2=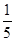 u.如果将3万元资金投入经营甲、乙两种商品,其中对甲商品的投资为x(万元).
u.如果将3万元资金投入经营甲、乙两种商品,其中对甲商品的投资为x(万元).
(1)求经营甲、乙两种商品的总利润y(万元)与x的函数关系式,并直接写出自变量x的取值范围;
(2)设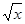 =t,试写出y关于t的函数关系式,并求出经营甲、乙两种商品各投入多少万元时使得总利润最大.
=t,试写出y关于t的函数关系式,并求出经营甲、乙两种商品各投入多少万元时使得总利润最大.
【答案】
(1)y= +
+ (3-x)(0≤x≤3);(2)甲、乙分别投入
(3-x)(0≤x≤3);(2)甲、乙分别投入 、
、 万元时
万元时
【解析】
试题分析:(1)对甲种商品投资x(万元),对乙种商品投资(3-x)(万元),根据经验公式可得甲、乙两种商品的总利润y(万元)关于x的函数表达式;
(2)利用配方法确定函数的对称轴,结合函数的定义域,即可求得总利润y的最大值.
(1)由已知y1= ,y2=
,y2= (3-x)
(3-x)
∴y=y1+y2= +
+ (3-x)
(3-x)
自变量x的的取值范围为0≤x≤3;
(2)∵ =t,∴x=t2,
=t,∴x=t2,
∴y= +
+ (3-t2)=-
(3-t2)=- t2+
t2+ +
+ =-
=- ( t-
( t- )2+
)2+
∴当t= 时,y取最大值.
时,y取最大值.
由t= 得,x=
得,x=
∴3-x=
即经营甲、乙两种商品分别投入 、
、 万元时,使得总利润最大.
万元时,使得总利润最大.
考点:二次函数的应用
点评:二次函数的应用是初中数学的重点和难点,在中考中极为常见,一般压轴题形式出现,难度较大.

练习册系列答案
相关题目
商场销售甲、乙两种商品,它们的进价和售价如下表所示,
(1)若该商场购进甲、乙两种商品共100件,恰好用去2700元,求购进甲、乙两种商品各多少件?
(2)该商场为使销售甲、乙两种商品共100件总利润(利润=售价-进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案.
(3)若商场销售甲、一两种商品的总利润(利润=售价-进价)是103元,求销售甲、乙两种商品多少件?
| 进价(元) | 售价(元) | |
| 甲 | 15 | 20 |
| 乙 | 35 | 43 |
(2)该商场为使销售甲、乙两种商品共100件总利润(利润=售价-进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案.
(3)若商场销售甲、一两种商品的总利润(利润=售价-进价)是103元,求销售甲、乙两种商品多少件?
商场销售甲、乙两种商品,它们的进价和零售价如下表所示:
(1)若该商场购进甲、乙两种商品共80件,恰好用去11400元,求购进甲、乙两种商品各多少件?
(2)该商场为使销售甲、乙两种商品共100件的总利润(利润=售价-进价)不少于3750元,且不超过3800元,请你帮助该商场设计相应的进货方案;
(3)若商场销售甲、乙两种商品的总利润是515元,求销售甲、乙两种商品各多少件?
| 进价(元) | 售价(元) | |
| 甲 | 75 | 100 |
| 乙 | 175 | 215 |
(2)该商场为使销售甲、乙两种商品共100件的总利润(利润=售价-进价)不少于3750元,且不超过3800元,请你帮助该商场设计相应的进货方案;
(3)若商场销售甲、乙两种商品的总利润是515元,求销售甲、乙两种商品各多少件?
商场销售甲、乙两种商品,它们的进价和售价如下表所示,
| 进价(元) | 售价(元) | |
| 甲 | 15 | 20 |
| 乙 | 35 | 43 |
(2)该商场为使销售甲、乙两种商品共100件总利润(利润=售价-进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案.
(3)若商场销售甲、一两种商品的总利润(利润=售价-进价)是103元,求销售甲、乙两种商品多少件?
商场销售甲、乙两种商品,它们的进价和零售价如下表所示:
| 进价(元) | 售价(元) | |
| 甲 | 75 | 100 |
| 乙 | 175 | 215 |
(2)该商场为使销售甲、乙两种商品共100件的总利润(利润=售价-进价)不少于3750元,且不超过3800元,请你帮助该商场设计相应的进货方案;
(3)若商场销售甲、乙两种商品的总利润是515元,求销售甲、乙两种商品各多少件?