题目内容
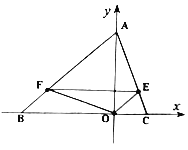
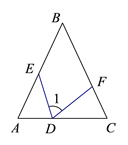
【题目】如图,菱形ABCD中,E,F分别为AD,AB上的点,且AE=AF,连接EF并延长,交CB的延长线于点G,连接BD.
(1) 求证:四边形EGBD是平行四边形;
(2) 连接AG,若∠FGB=![]() ,GB=AE=3,求AG的长.
,GB=AE=3,求AG的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)依据菱形的性质及等式的性质,得![]() ,
,![]() ,由平行得
,由平行得![]() ∽
∽![]() ,依据相似的性质得到
,依据相似的性质得到![]() ,从而
,从而![]() ,依据一组对边平行且相等的四边形是平行四边形得到四边形EGBD是平行四边形;
,依据一组对边平行且相等的四边形是平行四边形得到四边形EGBD是平行四边形;
(2)先结合条件求得![]() =3,
=3,![]() ,由等边对等角得到
,由等边对等角得到![]() ,依据三角形外角的性质得到
,依据三角形外角的性质得到![]() ,作
,作![]() 于
于![]() ,运用锐角三角函数求出
,运用锐角三角函数求出![]() ,再求出
,再求出![]() ,最后用勾股定理求出AG的长.
,最后用勾股定理求出AG的长.
解:(1) 证明:∵菱形ABCD,
∴![]() ,
,![]() ,
,
又∵AE=AF,
∴![]() ,即
,即![]() ,
,![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴四边形EGBD是平行四边形;
(2) ∵![]() ,GB=AE=3,AE=AF,
,GB=AE=3,AE=AF,
∴![]() =3,
=3,
∴![]() ,
,![]()
∴![]() ,
,
作![]() 于
于![]() ,
,
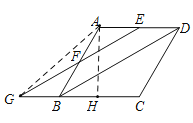
则![]() =
=![]() ,
,![]() =3,则
=3,则![]() ,
,
![]() =
=![]() =
=![]() .
.

练习册系列答案
相关题目