题目内容
已知如图，梯形ABCD的面积是4cm2，M为CD中点，连AM，BM，则△ABM的面积是________．
2cm2
分析：首先作辅助线：延长AM交BC的延长线于点N，然后利用梯形的性质，即可证得△ADM≌△NCM（AAS），根据全等三角形的性质得出S△ADM=S△NCM，再根据AM=MN=
AN求出S△ABN，最后根据S△ABM=S△ABN即可求得△ABM的面积；
解答：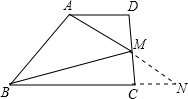
解：延长AM交BC的延长线于点N，
∵AD∥BC，
∴∠DAM=∠N，∠D=∠MCN，
∵点M是边CD的中点，
∴DM=CM，
∴在△ADM和△NCM中，
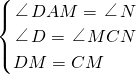
∴△ADM≌△NCM（AAS），
∴S△ADM=S△NCM，AM=MN=AN，
∴S△ABN=S梯形ABCD=4，
∴S△ABM=S△ABN=×4=2；
∴△ABM的面积是2cm2．
故填：2cm2．
点评：此题考查了梯形的性质与全等三角形的判定与性质，此题综合性比较强，同学们应该多做积累，解题的关键是注意数形结合思想的应用，注意辅助线的作法．
分析：首先作辅助线：延长AM交BC的延长线于点N，然后利用梯形的性质，即可证得△ADM≌△NCM（AAS），根据全等三角形的性质得出S△ADM=S△NCM，再根据AM=MN=
AN求出S△ABN，最后根据S△ABM=S△ABN即可求得△ABM的面积；解答：
解：延长AM交BC的延长线于点N，∵AD∥BC，
∴∠DAM=∠N，∠D=∠MCN，
∵点M是边CD的中点，
∴DM=CM，
∴在△ADM和△NCM中，
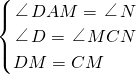
∴△ADM≌△NCM（AAS），
∴S△ADM=S△NCM，AM=MN=
AN，∴S△ABN=S梯形ABCD=4，
∴S△ABM=
S△ABN=×4=2；∴△ABM的面积是2cm2．
故填：2cm2．
点评：此题考查了梯形的性质与全等三角形的判定与性质，此题综合性比较强，同学们应该多做积累，解题的关键是注意数形结合思想的应用，注意辅助线的作法．
练习册系列答案
名校课堂系列答案
相关题目
（2012•通州区一模）已知如图，在△ABC中，AB=AC，∠ABC=α，将△ABC以点B为中心，沿逆时针方向旋转α度（0°＜α＜90°），得到△BDE，点B、A、E恰好在同一条直线上，连接CE．
.
S梯形ABCD ?若存在,请求出该点坐标,若不存在,请说明理由.
，请你求出四边形DBCE的面积.
，请你求出四边形DBCE的面积.
，请你求出四边形DBCE的面积.