题目内容
19.已知(x2-nx+5)(x2+x+7m)的展开式中不含x2和x3项,则m,n的值应该是( )| A. | m=$\frac{7}{4}$,n=1 | B. | m=$\frac{4}{7}$,n=-1 | C. | m=-$\frac{7}{4}$,n=1 | D. | m=-$\frac{4}{7}$,n=1 |
分析 原式利用多项式乘以多项式法则计算,合并后根据展开式中不含x2和x3项,即可求出m与n的值.
解答 解:(x2-nx+5)(x2+x+7m)
=x4+x3+7mx2-nx3-nx2-7mnx+5x2+5x+35m
=x4+(1-n)x3+(7m-n+5)x2+(-7mn+5)x+35m,
根据题意得:1-n=0,7m-n+5=0,
解得:m=-$\frac{4}{7}$,n=1.
故选D.
点评 本题考查了多项式乘以多项式,展开式中不含哪一项,就让哪一项的系数为0即可.

练习册系列答案
相关题目
7.某公园的门票价格规定如下表:
某校七年级甲、乙两个班共108人去游该公园,其中甲班人数较少,不到50人,乙班人数较多,有50多人.经估算,如果两班联合起来,作为一个团体购票,则一共应付1286元,问:
(1)两班各有学生多少人?
(2)如果两班联合起来,作为一个团体购票,可以省多少钱?
| 购票人数 | 1-50人 | 51-100人 | 100人以上 |
| 每人门票价 | 13元 | 11元 | 9元 |
(1)两班各有学生多少人?
(2)如果两班联合起来,作为一个团体购票,可以省多少钱?
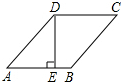 如图,在菱形ABCD中.DE⊥AB于E,DE=2,∠C=45°,则BE长是2$\sqrt{2}$-2.
如图,在菱形ABCD中.DE⊥AB于E,DE=2,∠C=45°,则BE长是2$\sqrt{2}$-2.