题目内容
【题目】如图，抛物线y= 
x2+ 
x﹣ 
（k＞0）与x轴交于点A、B，点A在点B的右边，与y轴交于点C
（1）如图1，若∠ACB=90°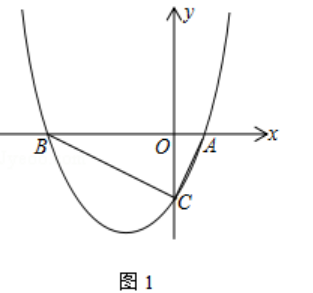
①求k的值；
②点P为x轴上方抛物线上一点，且点P到直线BC的距离为 
，则点P的坐标为（请直接写出结果）
（2）如图2，当k=2时，过原点O的任一直线y=mx（m≠0）交抛物线于点E、F（点E在点F的左边）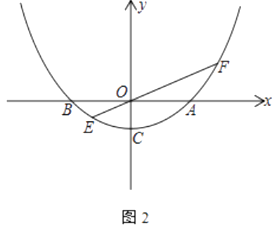
①若OF=2OE，求直线y=mx的解析式；
②求 
+ 
的值．
【答案】
（1）k=8；（﹣4﹣ 
， 
）
（2）
解：①过点E、F分别作x轴的垂线，垂直分别为M，N．
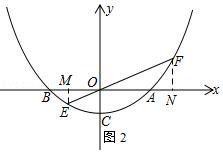
把k=2代入得：y= 
x2﹣1．
由 x2﹣1=mx，得到xE+xF=4m，xExF=﹣4．
∵OF=2OE，
∴xF=﹣2xE，且xE＜0，
∴﹣2xExE=﹣4，解得：xE=﹣ 
．
∴﹣ +2 =4m，解得：m= 
．
∴直线的解析式为y= x．
②设∠FON=α，则 
+ 
=cosα（ 
+ 
）．
∵直线EF的解析式为y=mx，
∴tanα=m，
∴cosα= 
．
∴ + = 
= 
= 
= 
．
∴ + =cosα（ + 
）= =1．
【解析】（1）①∵y= [x2+（k﹣2）x﹣2k]= （x﹣2）（x+k），
∴点A的坐标为（2，0），点B的坐标为（﹣k，0）．
∵将x=0代入抛物线的解析式为y=﹣ 
．
∴点C的坐标为（0，﹣ ）．
∵∠BCO+∠ACO=90°，∠OBC+∠BCO=90°，
∴∠OBC=∠OCA．
又∵∠BOC=∠AOC，
∴△OBC∽△OCA．
∴ 
= 
．
∴OC2=AOOB．
∴ k2=2k，解得：
k=8或者k=0（舍）
②将k=8代入抛物线的解析式得：y= x2+ 
x﹣4．
当x=0时，y=﹣4，
∴C（0，﹣4）．
令y=0得： x2+ x﹣4=0，解得x=﹣8或x=2．
∴A（2，0）B（﹣8，0）．
∴AC= 
=2 
．
设直线BC的解析式为y=kx+b，将点B和点C的坐标代入得： 
，
解得：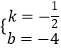 
，
∴直线BC的解析式为y= 
x﹣4．
设M为AC的中点，则M（1，﹣2），如图1所示：过点M作PM∥BC，交抛物线与点P．
设直线PM的解析式为y=﹣ 
x+c，将点M的坐标代入得：﹣ +c=﹣2，解得：c=﹣ ．
∴直线PM的解析式为y=﹣ x﹣ ．
∴﹣ x﹣ = x2+ x﹣4，解得x=﹣4﹣ 或x=﹣4+ （舍去）．
当x=﹣4﹣ 时，y= ．
∴点P的坐标为（﹣4﹣ ， ）．
所以答案是：（﹣4﹣ ， ）．
【考点精析】解答此题的关键在于理解根与系数的关系的相关知识，掌握一元二次方程ax2+bx+c=0（a≠0）的根由方程的系数a、b、c而定；两根之和等于方程的一次项系数除以二次项系数所得的商的相反数；两根之积等于常数项除以二次项系数所得的商，以及对确定一次函数的表达式的理解，了解确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法．
