题目内容
【题目】在平面直角坐标系中,![]() 的顶点坐标分别为
的顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
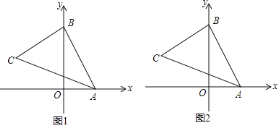
![]() 如图
如图![]() ,求
,求![]() 的面积.
的面积.
![]() 若点
若点![]() 的坐标为
的坐标为![]() ,
,
①请直接写出线段![]() 的长为________(用含
的长为________(用含![]() 的式子表示);
的式子表示);
②当![]() 时,求
时,求![]() 的值.
的值.
![]() 如图
如图![]() ,若
,若![]() 交
交![]() 轴于点
轴于点![]() ,直接写出点
,直接写出点![]() 的坐标为________.
的坐标为________.
【答案】(1)8,(2)①|m-2|②![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)过点C作CD⊥x轴,垂足为D,过点B作BE⊥CD,交DC延长线于E,过点A作AF⊥BE,交EB延长线于F,由题意得出∴D(-3,0),E(-3,4),F(2,4).得出AD=5,CD=2,BE=3,CE=2,DE=4,BF=2,AF=4.S△ABC=S矩形ADEF-S△ACD-S△BCE-S△ABF,即可得出结果;
(2)①根据题意容易得出结果;
②由三角形面积关系得出方程,解方程即可;
(3)与待定系数法求出直线AC的解析式,即可得出点D的坐标.
(1)过点C作CD⊥x轴,垂足为D,过点B作BE⊥CD,交DC延长线于E,
过点A作AF⊥BE,交EB延长线于F.如图所示:
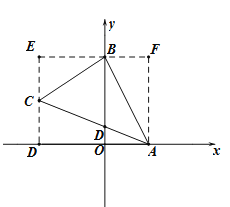
∵A(2,0),B(0,4),C(-3,2)
∴D(-3,0),E(-3,4),F(2,4).
∴AD=5,CD=2,BE=3,CE=2,DE=4,BF=2,AF=4.
∴S△ABC=S矩形ADEF-S△ACD-S△BCE-S△ABF
=ADDE ![]()
![]()
(2)①根据题意得:AP=|m-2|;
故答案为:|m-2|;
②∵![]()
∴![]()
∴![]() ,
,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ;
;
![]() 设直线
设直线![]() 的解析式为
的解析式为![]() ,
,
根据题意得:![]() ,
,
解得:![]() ,
,![]() ;
;
∴直线![]() 的解析式为
的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,;
,;
故答案为:![]() .
.

练习册系列答案
相关题目