题目内容
 如图,P是∠AOB平分线上一点,CD⊥OP于P,并分别交OA、OB于C,D,则点P到∠AOB两边距离之和
如图,P是∠AOB平分线上一点,CD⊥OP于P,并分别交OA、OB于C,D,则点P到∠AOB两边距离之和
- A.小于CD
- B.大于CD
- C.等于CD
- D.不能确定
A
分析:过点P作PE⊥OA于E,PF⊥OB于F,根据垂线段最短可得PE<PC,PF<PD,相加即可得解.
解答: 解:如图,过点P作PE⊥OA于E,PF⊥OB于F,
解:如图,过点P作PE⊥OA于E,PF⊥OB于F,
则PE、PF分别为点P到∠AOB两边的距离,
∵PE<PC,PF<PD,
∴PE+PF<PC+PD,
∴PE+PF<CD,
即点P到∠AOB两边距离之和小于CD.
故选A.
点评:本题主要考查了角平分线的性质,垂线段最短的性质,作出图形更形象直观.
分析:过点P作PE⊥OA于E,PF⊥OB于F,根据垂线段最短可得PE<PC,PF<PD,相加即可得解.
解答:
 解:如图,过点P作PE⊥OA于E,PF⊥OB于F,
解:如图,过点P作PE⊥OA于E,PF⊥OB于F,则PE、PF分别为点P到∠AOB两边的距离,
∵PE<PC,PF<PD,
∴PE+PF<PC+PD,
∴PE+PF<CD,
即点P到∠AOB两边距离之和小于CD.
故选A.
点评:本题主要考查了角平分线的性质,垂线段最短的性质,作出图形更形象直观.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 下面是小马虎解的一道题:
下面是小马虎解的一道题: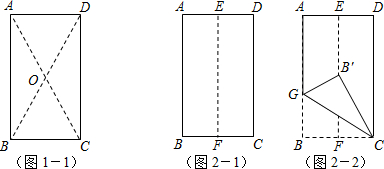
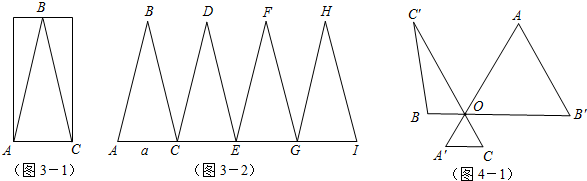
 (2012•开平区一模)如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数
(2012•开平区一模)如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数 如图,是一个平铺的某种儿童雨伞的伞面,它是由12块完全相同的等腰三角形布料缝合而成,量得其中一个三角形OAB的边OA=OB=40cm.则∠AOB=
如图,是一个平铺的某种儿童雨伞的伞面,它是由12块完全相同的等腰三角形布料缝合而成,量得其中一个三角形OAB的边OA=OB=40cm.则∠AOB= 下面是小民解的一道题,请你检查他的解答情况.
下面是小民解的一道题,请你检查他的解答情况.