题目内容
已知△ABC中,∠A=30°,∠B=45°,△ABC的面积为 ,若AC=m,则m的值为
,若AC=m,则m的值为
- A.1
- B.2
- C.

- D.

B
分析:作CD⊥AB于点D,利用AC的长表示出CD和AB的长,利用三角形的面积公式得到有关m的方程求解即可.
解答: 解:如图:作CD⊥AB于点D,
解:如图:作CD⊥AB于点D,
∵∠A=30°,∠B=45°,AC=m,
∴CD=BD=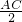 =
= ,
,
∴由勾股定理得:AD= m,
m,
∴AB=AD+BD= m
m
∵△ABC的面积为 ,
,
∴ AD•CD=
AD•CD= ,
,
即:
 m•
m• =
= ,
,
解得:m=±2.
故选B.
点评:本题考查了一元二次方程的应用,含30度角的直角三角形及勾股定理的知识,考查的知识点比较多,正确的作出图象是解题的关键.
分析:作CD⊥AB于点D,利用AC的长表示出CD和AB的长,利用三角形的面积公式得到有关m的方程求解即可.
解答:
 解:如图:作CD⊥AB于点D,
解:如图:作CD⊥AB于点D,∵∠A=30°,∠B=45°,AC=m,
∴CD=BD=
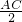 =
= ,
,∴由勾股定理得:AD=
 m,
m,∴AB=AD+BD=
 m
m∵△ABC的面积为
 ,
,∴
 AD•CD=
AD•CD= ,
,即:

 m•
m• =
= ,
,解得:m=±2.
故选B.
点评:本题考查了一元二次方程的应用,含30度角的直角三角形及勾股定理的知识,考查的知识点比较多,正确的作出图象是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 情况;若不可能,请说明理由.
情况;若不可能,请说明理由. 已知△ABC中,DE∥BC,EF∥AB,AB=3,BC=6,AD:DB=2:1,则四边形DBFE的周长为
已知△ABC中,DE∥BC,EF∥AB,AB=3,BC=6,AD:DB=2:1,则四边形DBFE的周长为 如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F
如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F 如图,已知△ABC中,AB=AC,AB垂直平分线交AC于D,连接BE,若∠A=40°,则∠EBC=( )
如图,已知△ABC中,AB=AC,AB垂直平分线交AC于D,连接BE,若∠A=40°,则∠EBC=( )