题目内容
【题目】如图，在△ABC中，AB=13cm，AC=12cm，BC=5cm．D是BC边上的一个动点，连接AD，过点C作CE⊥AD于E，连接BE，在点D变化的过程中，线段BE的最小值是__cm.
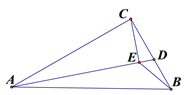
【答案】
【解析】如图，连接B
、BC. 在点D移动的过程中，点E在AC为直径的圆上运动，当
、E、B共线时，BE的值最小，最小值为
B-
E，利用勾股定理求出B
即可解决问题.
解：如图，以AC为直径作圆
，连接B
、E
.
∵CE⊥AD，
∴∠AEC=90°，
在△ABC中，AB=13cm，AC=12cm，BC=5cm，
AB2=AC2+BC2，
∴△ABC为Rt△，
在Rt△BC
中，B
=
，
∵
、E、B、共线时，BE的值最小，最小值为
B–
E=
– 6，
故答案为： 
– 6.
“点睛”本题考查圆综合题、勾股定点与圆的位置关系等知识，解题的关键是确定点E的运动轨迹，是以AC为直径的圆上运动，属于中考填空中压轴题.
练习册系列答案
相关题目
