题目内容
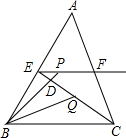 如图所示,在△ABC中,BC=6,E,F分别是AB,AC的中点,点P在射线EF上,BP交CE于D,点Q在CE上且BQ平分∠CBP,设BP=y,PE=x.当CQ=
如图所示,在△ABC中,BC=6,E,F分别是AB,AC的中点,点P在射线EF上,BP交CE于D,点Q在CE上且BQ平分∠CBP,设BP=y,PE=x.当CQ= CE时,y与x之间的函数关系式是________; 当CQ=
CE时,y与x之间的函数关系式是________; 当CQ= CE(n为不小于2的常数)时,y与x之间的函数关系式是________.
CE(n为不小于2的常数)时,y与x之间的函数关系式是________.
y=-x+6 y=-x+6(n-1)
分析:采用一般到特殊的方法.解答中首先给出一般性结论的证明,即当EQ=kCQ(k>0)时,y与x满足的函数关系式为:y=6k-x;然后将该关系式应用到本题中求解.在解题过程中,充分利用了相似三角形比例线段之间的关系.另外,利用角平分线上的点到角两边的距离相等的性质得出了一个重要结论④,该结论在解题过程中发挥了重要作用.
解答: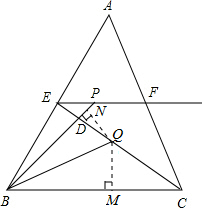 解:如右图,过Q点作QM⊥BC于点M,作QN⊥BP于点N.
解:如右图,过Q点作QM⊥BC于点M,作QN⊥BP于点N.
设CQ=a,DE=b,BD=c,则DP=y-c;
不妨设EQ=kCQ=ka(k>0),则DQ=ka-b,CD=(k+1)a-b.
∵BQ平分∠CBP,
∴QM=QN.
∴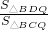 =
=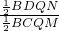 =
= ,
,
又∵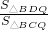 =
=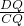 ,
,
∴ =
=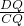 ,即
,即 =
=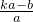 ①
①
∵EP∥BC,
∴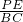 =
= ,即
,即 =
=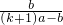 ②
②
∵EP∥BC,
∴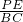 =
= ,即
,即 =
=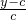 ③
③
将①②③式联立,解得:y=6k-x ④
当CQ= CE时,k=1,
CE时,k=1,
故y与x之间的函数关系式为:y=6-x;
当CQ= CE(n为不小于2的常数)时,k=n-1,由④式可知,
CE(n为不小于2的常数)时,k=n-1,由④式可知,
y与x之间的函数关系式为:y=6(n-1)-x.
故答案为y=-x+6;y=-x+6(n-1).
点评:本题综合考查了相似三角形线段之间的比例关系、角平分线的性质等重要知识点,难度较大.在解题过程中,涉及到数目较多的线段和较为复杂的运算,注意不要出错.本题采用了从一般到特殊的解题思想,简化了解答过程;同学们亦可尝试从特殊到一般的解题思路,即当CQ= CE时,CQ=
CE时,CQ= CE时分别探究y与x的函数关系式,然后推广到当CQ=
CE时分别探究y与x的函数关系式,然后推广到当CQ= CE(n为不小于2的常数)时的一般情况.
CE(n为不小于2的常数)时的一般情况.
分析:采用一般到特殊的方法.解答中首先给出一般性结论的证明,即当EQ=kCQ(k>0)时,y与x满足的函数关系式为:y=6k-x;然后将该关系式应用到本题中求解.在解题过程中,充分利用了相似三角形比例线段之间的关系.另外,利用角平分线上的点到角两边的距离相等的性质得出了一个重要结论④,该结论在解题过程中发挥了重要作用.
解答:
 解:如右图,过Q点作QM⊥BC于点M,作QN⊥BP于点N.
解:如右图,过Q点作QM⊥BC于点M,作QN⊥BP于点N.设CQ=a,DE=b,BD=c,则DP=y-c;
不妨设EQ=kCQ=ka(k>0),则DQ=ka-b,CD=(k+1)a-b.
∵BQ平分∠CBP,
∴QM=QN.
∴
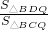 =
=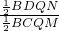 =
= ,
,又∵
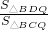 =
=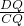 ,
,∴
 =
=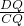 ,即
,即 =
=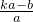 ①
①∵EP∥BC,
∴
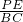 =
= ,即
,即 =
=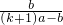 ②
②∵EP∥BC,
∴
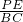 =
= ,即
,即 =
=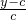 ③
③将①②③式联立,解得:y=6k-x ④
当CQ=
 CE时,k=1,
CE时,k=1,故y与x之间的函数关系式为:y=6-x;
当CQ=
 CE(n为不小于2的常数)时,k=n-1,由④式可知,
CE(n为不小于2的常数)时,k=n-1,由④式可知,y与x之间的函数关系式为:y=6(n-1)-x.
故答案为y=-x+6;y=-x+6(n-1).
点评:本题综合考查了相似三角形线段之间的比例关系、角平分线的性质等重要知识点,难度较大.在解题过程中,涉及到数目较多的线段和较为复杂的运算,注意不要出错.本题采用了从一般到特殊的解题思想,简化了解答过程;同学们亦可尝试从特殊到一般的解题思路,即当CQ=
 CE时,CQ=
CE时,CQ= CE时分别探究y与x的函数关系式,然后推广到当CQ=
CE时分别探究y与x的函数关系式,然后推广到当CQ= CE(n为不小于2的常数)时的一般情况.
CE(n为不小于2的常数)时的一般情况. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在△ABC中,∠A=47°,∠C=77°,DE∥BC,BF平分∠ABC,BF交DE于点F,求∠BFE的度数.
如图所示,在△ABC中,∠A=47°,∠C=77°,DE∥BC,BF平分∠ABC,BF交DE于点F,求∠BFE的度数.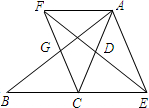 如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF.
如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF. 15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=
15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=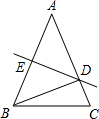 如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为
如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为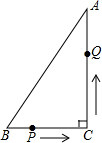 如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.
如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.