Question

如图，一个4×2的矩形可以用3种不同的方式分割成2或5或8个小正方形，

（1）一个3×2的矩形用不同的方式分割后，小正方形的个数可以是______；画出相应的图形．
（2）一个5×2的矩形用不同的方式分割后，小正方形的个数可以是______；画出相应的图形．
（3）一个n×2的矩形用不同的方式分割后，小正方形的个数最多是______；小正方形的个数最少是______（直接填写结果）
（4）一个4×3的矩形用不同的方式分割后，小正方形的个数可以是______．

Answer 1

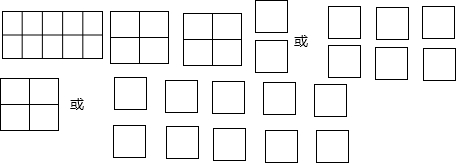
解：（1）一个3×2的矩形用不同的方式分割后，小正方形的个数可以是3或6，作图如下：
（2）一个5×2的矩形用不同的方式分割后，小正方形的个数可以是4或7或10，作图如下：

（3）一个n×2的矩形用不同的方式分割后，小正方形的个数最多是 2n；小正方形的个数最少是 ①n为偶数，有个；②n为奇数，有个；
（4）一个4×3的矩形用不同的方式分割后，小正方形的个数可以是 4或6或9或12．
故答案为：3或6；4或7或10；2n；①n为偶数，有个；②n为奇数，有个；4或6或9或12．
分析：（1）一个3×2的矩形可以是1个2×2和2个1×1或6个1×1的．
（2）一个5×2的矩形可以是2个2×2和2个1×1或1个2×2和6个1×1或10个1×1的．
（3）一个n×2的矩形用不同的方式分割后，小正方形都是1×1的小正方形的个数最多，分奇偶性讨论小正方形的个数最少的情况；
（4）一个4×3的矩形可以是1个3×3和3个1×1或2个2×2和4个1×1或1个2×2和8个1×1或12个1×1的．
点评：本题考查了规律型：图形的变化，关键是通过归纳与总结，得到其中的规律．正方形可以是1×1的或2×2的或3×3的．