题目内容
 (2013•陕西)如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则
(2013•陕西)如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则| AM |
| MD |
分析:首先由菱形的四条边都相等与矩形的四个角是直角,即可得到直角△ABE中三边的关系.
解答:解:∵四边形MBND是菱形,
∴MD=MB.
∵四边形ABCD是矩形,
∴∠A=90°.
设AB=x,AM=y,则MB=2x-y,(x、y均为正数).
在Rt△ABM中,AB2+AM2=BM2,即x2+y2=(2x-y)2,
解得x=
y,
∴MD=MB=2x-y=
y,
∴
=
=
.
故选C.
∴MD=MB.
∵四边形ABCD是矩形,
∴∠A=90°.
设AB=x,AM=y,则MB=2x-y,(x、y均为正数).
在Rt△ABM中,AB2+AM2=BM2,即x2+y2=(2x-y)2,
解得x=
| 4 |
| 3 |
∴MD=MB=2x-y=
| 5 |
| 3 |
∴
| AM |
| MD |
| y | ||
|
| 3 |
| 5 |
故选C.
点评:此题考查了菱形与矩形的性质,以及直角三角形中的勾股定理.解此题的关键是注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 (2013•陕西)如图,下面的几何体是由一个圆柱和一个长方体组成的,则它的俯视图是( )
(2013•陕西)如图,下面的几何体是由一个圆柱和一个长方体组成的,则它的俯视图是( ) (2013•陕西)如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D的大小为( )
(2013•陕西)如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D的大小为( ) (2013•陕西)如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有( )
(2013•陕西)如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有( )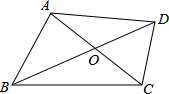 (2013•陕西)如图,四边形ABCD的对角线AC,BD相交于点O,且BD平分AC.若BD=8,AC=6,∠BOC=120°,则四边形ABCD的面积为
(2013•陕西)如图,四边形ABCD的对角线AC,BD相交于点O,且BD平分AC.若BD=8,AC=6,∠BOC=120°,则四边形ABCD的面积为 (2013•陕西)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为
(2013•陕西)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为