题目内容
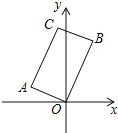
【题目】如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,求B、C两点的坐标.
【答案】B(![]() ,3),C(﹣
,3),C(﹣![]() ,4).
,4).
【解析】
试题分析:首先过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CF∥y轴,过点A作AF∥x轴,交点为F,易得△CAF≌△BOE,△AOD∽△OBE,然后由相似三角形的对应边成比例,求得答案.
解:过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CF∥y轴,过点A作AF∥x轴,交点为F,延长CA交x轴于点H,
∵四边形AOBC是矩形,
∴AC∥OB,AC=OB,
∴∠CAF=∠BOE=∠CHO,
在△ACF和△OBE中,
 ,
,
∴△CAF≌△BOE(AAS),
∴BE=CF=4﹣1=3,
∵∠AOD+∠BOE=∠BOE+∠OBE=90°,
∴∠AOD=∠OBE,
∵∠ADO=∠OEB=90°,
∴△AOD∽△OBE,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴OE=![]() ,
,
即点B(![]() ,3),
,3),
∴AF=OE=![]() ,
,
∴点C的横坐标为:﹣(2﹣![]() )=﹣
)=﹣![]() ,
,
∴点C(﹣![]() ,4).
,4).


练习册系列答案
相关题目