题目内容
如图,△ABC是边长为3的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连接BD,交AC于F.(8分)
(1)猜想AC与BD的位置关系,并证明你的结论;
(2)求线段BD的长.
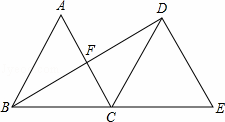
解:(1)AC⊥BD∵△DCE由△ABC平移而成,
∴BE=2BC=6,DE=AC=3,∠E=∠ACB=60°,
∴DE=BE,
∵BD⊥DE,
∵∠E=∠ACB=60°,
∴AC∥DE,
∴BD⊥AC;
(2)在Rt△BED中,
∵BE=6,DE=3,
∴BD=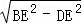 =
=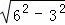 =3
=3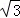 .
.

练习册系列答案
相关题目
现有边长相等的正三角形、正方形、正六边形、正八边形形状的地砖,如果选择其中的两种铺满平整的地面,那么选择的两种地砖形状不能是( )
|
| A. | 正三角形与正方形 | B. | 正三角形与正六边形 |
|
| C. | 正方形与正六边形 | D. | 正方形与正八边形 |
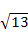 个单位长度,请在网格中作出平移后的图形;
个单位长度,请在网格中作出平移后的图形;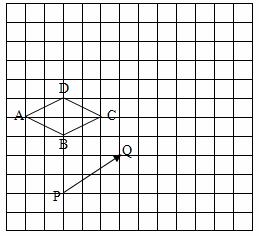
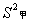 ______
______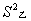 (填“<”,“=”,“>”).
(填“<”,“=”,“>”).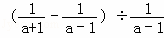 ,其中a=
,其中a=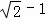 .(6分)
.(6分)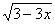 的自变量
的自变量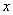 的取值范围是 .
的取值范围是 .