题目内容
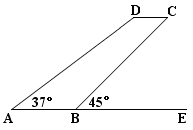
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=12 .
.

求:(1)BC的长;(2)CD的长.
 .
. 
求:(1)BC的长;(2)CD的长.
(1)12 ;(2)12-4
;(2)12-4
 ;(2)12-4
;(2)12-4
试题分析:(1)由题意可知△ACB为等腰直角三角形,根据等腰直角三角形的性质求解即可;
(2)过点B作BM⊥FD于点M,根据平行线的性质可求得BM、CM的长,再在△EFD中,根据三角形的内角和定理求得∠EDF=60°,根据∠EDF的正切函数即可求得MD的长,从而可以求得结果.
(1)在△ACB中,∠ACB=90°,∠A=45°,AC=12
 ,
,∴BC=AC=12
 ;
;(2)过点B作BM⊥FD于点M,

∵AB∥CF,
∴BM=BC×sin45°=12
 ×
× =12,CM=BM=12.
=12,CM=BM=12.在△EFD中,∠F=90°,∠E=30°,
∴∠EDF=60°,
∴MD=BM÷tan60°=4
 ,
,∴CD=CM-MD=12-4
 .
.点评:解直角三角形的应用是中考必考题,一般难度不大,正确作出辅助线构造直角三角形是解题关键.

练习册系列答案
相关题目

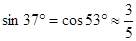 ,
,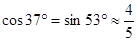 ,
,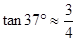 )
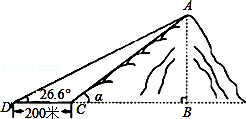
)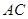 的坡度是
的坡度是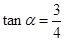 ,在与山脚
,在与山脚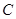 距离
距离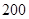 米的
米的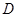 处,测得山顶
处,测得山顶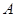 的仰角为
的仰角为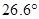 ,求小山岗的高
,求小山岗的高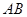 (结果取整数:参考数据:
(结果取整数:参考数据: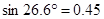 ,
,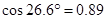 ,
,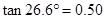 ).
).

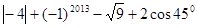
 ≈1.732).
≈1.732).
