题目内容
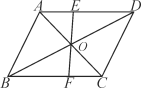
【题目】如图，在四边形ABCD中，AB⊥BC，AB∥DC，AB，BC，CD分别为2,2,2
＋2，则∠BAD的度数等于( )
A. 120° B. 135° C. 150° D. 以上都不对
【答案】C
【解析】
过A作AE⊥CD于E，得出四边形ABCE是矩形，根据矩形的性质求出AB=CE=2，AE=BC=2，∠BAE=90°，根据勾股定理求出AD=4，即可求出∠DAE的度数，求出答案即可．
过A作AE⊥CD于E．
∵AB⊥BC，AB∥DC，∴∠B=∠C=∠AED=∠AEC=90°，∴四边形ABCE是矩形，∴AB=CE=2，AE=BC=2，∠BAE=90°．
∵CD=2
2，∴DE=2
，由勾股定理得：AD=4=2AE，∴∠D=30°，∠DAE=60°．
∵∠BAE=90°，∴∠BAD=90°+60°=150°．
故选C．
练习册系列答案
相关题目
【题目】随着“互联网+”时代的到来，一种新型打车方式受到大众欢迎，该打车方式的总费用由里程费和耗时费组成，其中里程费按
元/公里计算，耗时费按
元/分钟计算(总费用不足
元按元计价)．小敏、小刚两人用该打车方式出行，按上述计价规则，其行驶里程数、耗时以及打车总费用如下表：
里程数 | 耗时 | 车费(元) | |
小敏 |
|
|
|
小刚 |
|
|
|
求
的值；
若小华也用该打车方式打车，平均车速为
公里/时，行驶了
