题目内容
已知Rt△ABC，∠A=90°（1）请画出它的外接圆．
（2）计算：若AC=5，AB=12，求外接圆的半径．
分析：（1）先作AB的垂直平分线交BC于点P，然后以点P为圆心，以PB为半径画圆，则⊙P就是△ABC的外接圆；
（2）根据勾股定理求出BC的长度，然后半径可得．
（2）根据勾股定理求出BC的长度，然后半径可得．
解答：解：（1）如图所示，⊙P就是△ABC的外接圆；
（2）在Rt△ABC中，∵AC=5，AB=12，
∴BC=
=
=13，
13÷2=6.5，
∴外接圆的半径是6.5．
（2）在Rt△ABC中，∵AC=5，AB=12，
∴BC=
| AC2+AB2 |
| 52+122 |
13÷2=6.5，
∴外接圆的半径是6.5．
点评：本题主要考查了三角形的外心的作法，勾股定理，熟练掌握线段垂直平分线的作法是解题的关键．
练习册系列答案
相关题目
已知Rt△ABC中，∠C=90°，AC=8cm，BC=6cm．则其内心和外心之间的距离是（ ）
| A、10cm | ||
| B、5cm | ||
C、
| ||
| D、2cm |
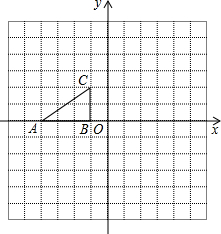如图，每个小方格都是边长为1个单位的正方形．Rt△ABC 的顶点在格 点上，建立平面直角坐标系后，点A的坐标为（-4，0），点B的坐标为（-1，0）．已知Rt△ABC和Rt△A1B1C1关于y轴对称，Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称．