题目内容
在△ABC中,D在AB上,且DE∥BC,| AD |
| DB |
| 1 |
| 2 |
分析:根据DE∥BC,可以求证△ADE∽△ABC,即可求得△ADE与△ABC面积的比值,即可解题.
解答:解:∵DE∥BC,
∴△ADE∽△ABC且相似比为1;3,
∴△ADE与△ABC的面积比为(
)2,
△ABC的面积为9,则△ADE的面积为1,
故答案为 1.
∴△ADE∽△ABC且相似比为1;3,
∴△ADE与△ABC的面积比为(
| 1 |
| 3 |
△ABC的面积为9,则△ADE的面积为1,
故答案为 1.
点评:本题考查了相似三角形对应边比值相等的性质,考查了相似三角形的判定,本题中根据△ADE和△ABC对应比求其面积的比是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
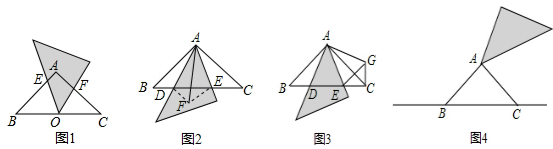
 其他字母和辅助线,找结论过程中添加的字母和辅助线不能出现在结论中,不必证明)
其他字母和辅助线,找结论过程中添加的字母和辅助线不能出现在结论中,不必证明)


