题目内容
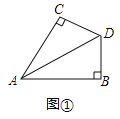
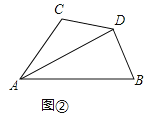
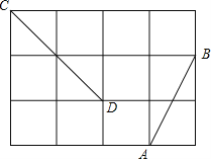
【题目】如图在
中，
，
、
分别是
、
的平分线，、相交于点
．
（1）请你判断并写出
与
之间的数量关系；
（2）试判断线段
、
与
之间的数量关系并说明理由．
【答案】（1）
；（2）
，见解析
【解析】
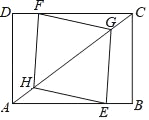
（1）在
上截取
，利用SAS证出
，从而得出
，
，然后利用ASA证出
，从而得出
，即可得出结论；
（2）根据（1）中两个全等三角形可得
，
，从而证出结论．
解：（1）
与
的关系是，
在上截取，
、
分别是
、
的平分线，
，
在△AEF和△AHF中
，
，
∵∠B=60°
∴∠BAC＋∠BCA=180°－∠B=120°
∵、分别是、的平分线，
∴∠FAC＋∠FCA=
＋
=
=60°
∴
180°－（∠FAC＋∠FCA）=120°，
=∠FAC＋∠FCA=60°
，
，
，
在△CFH和△CFD中
，
，
（2）
理由：由（1）知：
，
，
，
即
练习册系列答案
相关题目
【题目】弹簧原长(不挂重物)15cm，弹簧总长L(cm)与重物质量x(kg)的关系如下表所示：
弹簧总长L(cm) | 16 | 17 | 18 | 19 | 20 |
重物质量x(kg) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
当重物质量为4kg（在弹性限度内）时，弹簧的总长L(cm)是_________．
