题目内容
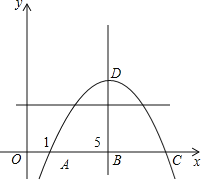
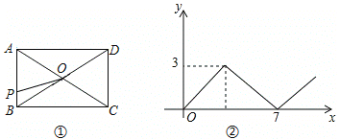
【题目】在矩形ABCD中，AB＜AD，对角线AC，BD相交于点O，动点P由点A出发，沿AB→BC→CD向点D运动．设点P的运动路程为x，△AOP的面积为y，y与x的函数关系图象如图②所示，则AD边的长为（ ）
A.3B.4C.5D.6
【答案】B
【解析】
结合图象与矩形根据三角形的面积公式求得ABBC＝12，根据图象与矩形得到当点P运动到点C时y为0，由此得到AB+BC＝7，由此解一元二次方程即可求出答案.
解：当P点在AB上运动时，y逐渐增大，当P点到达B点时，y最大为3．
∴
ABBC＝3，即ABBC＝12．
当P点在BC上运动时，y逐渐减小，当P点到达C点时，y为0，此时结合图象可知P点运动路径长为7，
∴AB+BC＝7．
则BC＝7﹣AB，代入ABBC＝12，
得：AB2﹣7AB+12＝0，
解得：AB＝4或3，
∵AB＜AD，
∴AB＝3，BC＝4．
即AD=BC=4，
故答案为：B.
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表所示：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法中，错误的是（ ）
A. 抛物线于x轴的一个交点坐标为（﹣2，0）
B. 抛物线与y轴的交点坐标为（0，6）
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
【题目】目前“微信”以其颠覆性的创新，赢得了数亿人的支持，为了调查某中学学生在周日上“微信”的时间，随机对100名男生和100名女生进行了问卷调查，得到了如下的统计结果
表1：男生上“微信时间的频数分布表
上网时间（分钟） | 30≤x＜40 | 40≤x＜50 | 50≤x＜60 | 60≤x＜70 | 70≤x＜80 |
人数 | 5 | 25 | 30 | 25 | 15 |
表2：女生上“微信”时间的频数分布表
上网时间（分钟） | 30≤x＜40 | 40≤x＜50 | 50≤x＜60 | 60≤x＜70 | 70≤x＜80 |
人数 | 10 | 20 | 40 | 20 | 10 |
请结合图表完成下列各题
（1）完成表3：
表3 | 上“微信”时间少于60分钟 | 上“微信”时间不少于60分钟 |
男生人数 |
|
|
女生人数 |
|
|
（2）若该中学共有女生750人，请估计其中上“微信”时间不少于60分钟的人数；
（3）从表3的男生中抽取5人（其中3人上“微信”时间少于60分钟，2人上“微信”时间不少于60分钟），再从抽取的5人中任取2人，请用列表或画树状图的方法求出至少有一人上“微信”时间不少于60分钟的概率．
