题目内容
【题目】甲、乙两人进行羽毛球比赛，把球看成点，其飞行的路线为抛物线的一部分．如图建立平面直角坐标系，甲在O点正上方1m的P处发球，羽毛球飞行的高度y（m）与羽毛球距离甲站立位置（点O）的水平距离x（m）之间满足函败表达式y＝a（x﹣4）2+h．已知点O与球网的水平距离为5m，球网的高度为1.55m，球场边界距点O的水平距离为10m．
（1）当a＝﹣
时，求h的值，并通过计算判断此球能否过网．
（2）若甲发球过网后，乙在另一侧距球网水平距离lm处起跳扣球没有成功，球在距球网水平距离lm，离地面高度2.2m处飞过，通过计算判断此球会不会出界？
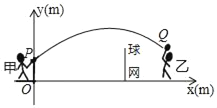
【答案】（1）球能过网；（2）此球不会出界．
【解析】
（1）①将点P（0，1）代入y=﹣
（x-4）2+h即可求得h；②求出x=5时，y的值，与1.55比较即可得出判断；
（2）将（0，1）、（6，2.2）代入y=a（x-4）2+h代入即可求得a、h，得出关系式，求出x=10时，y的值比较即可判断
（1）当a＝﹣
时，y＝﹣（x﹣4）2+h，
将点P（0，1）代入得：1＝﹣（﹣4）2+h，
解得：h＝
，
∴y＝﹣（x﹣4）2+，
当x＝5时，y＝﹣×（5﹣4）2+＝
，
∵＝1.75＞1.55，
∴球能过网．
（2）由题意知，球过P（0，1）、（6，2.2）两点，
则
，
解得：
，
所以y＝﹣
（x﹣4）2+
，
当x＝10时，y＝﹣（10﹣4）2+＝﹣1＜0，
∴此球不会出界．
【题目】在不透明的袋子中有四张标有数字1，2，3，4的卡片，小明、小华两人按照各自的规则玩抽卡片游戏。
小明画出树形图如下：
小华列出表格如下：
第一次 第二次 | 1 | 2 | 3 | 4 |
1 | （1，1） | （2，1） | （3，1） | （4，1） |
2 | （1，2） | （2，2） | ① | （4，2） |
3 | （1，3） | （2，3） | （3，3） | （4，3） |
4 | （1，4） | （2，4） | （3，4） | （4，4） |
回答下列问题：
（1）根据小明画出的树形图分析，他的游戏规则是：随机抽出一张卡片后 （填“放回”或“不放回”），再随机抽出一张卡片；
（2）根据小华的游戏规则，表格中①表示的有序数对为 ；
（3）规定两次抽到的数字之和为奇数的获胜，你认为淮获胜的可能性大？为什么？
