题目内容
计算或化简:
(1)
(2)
(3)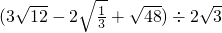
(4)sin230°+cos245°+sin60°•tan45°.
解:
(1) ,
,
=(2 +
+ )(
)( -2
-2 ),
),
=(2 +2
+2 )(2
)(2 -2
-2 ),
),
=(2 )2-(2
)2-(2 )2,
)2,
=12-20,
=-8;
(2) ,
,
=3 -
- ×
× -
- ×m
×m ,
,
=3 -
- -
- ,
,
=(3- -
- )
) ,
,
= ;
;
(3)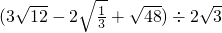 ,
,
=(3× -2×
-2× +4
+4 )÷2
)÷2 ,
,
= ÷2
÷2 ,
,
= ;
;
(4)sin230°+cos245°+sin60°•tan45°,
=( )2+(
)2+( )2+
)2+ ×1,
×1,
= +
+ +
+ ,
,
= +
+ ,
,
=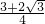 .
.
分析:(1)化简二次根式后,再运用平方差公式求出比较简单;
(2)把二次根式化为最简二次根式,再进行合并同类二次根式即可得出答案;
(3)把二次根式化为最简二次根式,再进行合并同类二次根式,然后进行除法运算,即可得出答案;
(4)先把特殊角的三角函数值代入原式,然后再计算.
点评:此题主要考查了特殊角的三角函数值以及二次根式的混合运算,在进行二次根式的计算时,要先把二次根式化为最简二次根式再进行计算以及正确记忆特殊角三角函数值是解决问题的关键.
(1)
 ,
,=(2
 +
+ )(
)( -2
-2 ),
),=(2
 +2
+2 )(2
)(2 -2
-2 ),
),=(2
 )2-(2
)2-(2 )2,
)2,=12-20,
=-8;
(2)
 ,
,=3
 -
- ×
× -
- ×m
×m ,
,=3
 -
- -
- ,
,=(3-
 -
- )
) ,
,=
 ;
;(3)
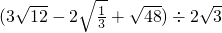 ,
,=(3×
 -2×
-2× +4
+4 )÷2
)÷2 ,
,=
 ÷2
÷2 ,
,=
 ;
;(4)sin230°+cos245°+sin60°•tan45°,
=(
 )2+(
)2+( )2+
)2+ ×1,
×1,=
 +
+ +
+ ,
,=
 +
+ ,
,=
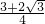 .
.分析:(1)化简二次根式后,再运用平方差公式求出比较简单;
(2)把二次根式化为最简二次根式,再进行合并同类二次根式即可得出答案;
(3)把二次根式化为最简二次根式,再进行合并同类二次根式,然后进行除法运算,即可得出答案;
(4)先把特殊角的三角函数值代入原式,然后再计算.
点评:此题主要考查了特殊角的三角函数值以及二次根式的混合运算,在进行二次根式的计算时,要先把二次根式化为最简二次根式再进行计算以及正确记忆特殊角三角函数值是解决问题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目