Question

【题目】已知，抛物线y＝x2﹣x+与x轴分别交于A、B两点（A点在B点的左侧），交y轴于点F．

（1）A点坐标为　 　；B点坐标为　 　；F点坐标为　 　；

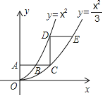
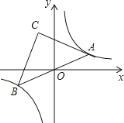
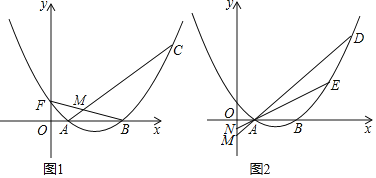
（2）如图1，C为第一象限抛物线上一点，连接AC，BF交于点M，若BM＝FM，在直线AC下方的抛物线上是否存在点P，使S△ACP＝4，若存在，请求出点P的坐标，若不存在，请说明理由；

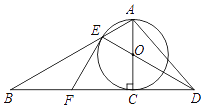
（3）如图2，D、E是对称轴右侧第一象限抛物线上的两点，直线AD、AE分别交y轴于M、N两点，若OMON＝，求证：直线DE必经过一定点．

Answer 1

【答案】（1）（1，0），（3，0），（0，）；（2）在直线AC下方的抛物线上不存在点P，使S△ACP＝4，见解析；（3）见解析

【解析】

（1）根据坐标轴上点的特点建立方程求解，即可得出结论；

（2）在直线AC下方轴x上一点，使S△ACH＝4，求出点H坐标，再求出直线AC的解析式，进而得出点H坐标，最后用过点H平行于直线AC的直线与抛物线解析式联立求解，即可得出结论；

（3）联立直线DE的解析式与抛物线解析式联立，得出，进而得出，，再由得出，进而求出，同理可得，再根据，即可得出结论．

（1）针对于抛物线，

令x＝0，则，

∴，

令y＝0，则，

解得，x＝1或x＝3，

∴，

综上所述：,,；

（2）由（1）知，，，

∵BM＝FM，

∴，

∵，

∴直线AC的解析式为：，

联立抛物线解析式得：，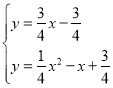

解得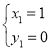：或，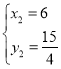

∴，

如图1，设H是直线AC下方轴x上一点，AH＝a且S△ACH＝4，

∴，

解得：，

∴，

过H作l∥AC，

∴直线l的解析式为，

联立抛物线解析式，解得，

∴，

即：在直线AC下方的抛物线上不存在点P，使；

（3）如图2，过D，E分别作x轴的垂线，垂足分别为G，H，

设，，直线DE的解析式为，

联立直线DE的解析式与抛物线解析式联立，得，

∴，，

∵DG⊥x轴，

∴DG∥OM，

∴，

∴，

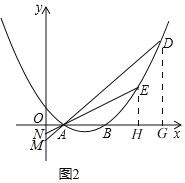
即，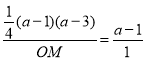

∴，同理可得

∴，

∴，

即，

∴，

∴直线DE的解析式为，

∴直线DE必经过一定点．