题目内容
梯形ABCD中，AD∥BC，则∠A：∠B：∠C：∠D的值可能是
- A.4：6：2：8
- B.2：4：6：8
- C.4：2：8：6
- D.8：4：2：6
A
分析：根据梯形的性质利用四边形的内角和公式对各个选项进行分析从而得到最后答案．
解答：由梯形的性质知，∠A与∠B互补，∠C与∠D互补，则，∠A与∠B的和，∠C与∠D的和均为180°，
设四角的度数分别为：4X，6X，2X，8X，由四边形的内角和为360°，
得4X+6X+2X+8X=360°，解得，四角分别为：72°，108°，72°，144°，
同理B中的四角分别为：36°，72°，108°，144°，
同理C中的四角分别为：72°，36°，108°，150°，
同理D中的四角分别为：144°，72°，36°，108°，
所以只有A中的满足∠A与∠B互补，∠C与∠D互补，
故选A．
点评：本题通过设适当的参数，根据四边形的内角和建立方程，求得各角的度数进行判定．
分析：根据梯形的性质利用四边形的内角和公式对各个选项进行分析从而得到最后答案．
解答：由梯形的性质知，∠A与∠B互补，∠C与∠D互补，则，∠A与∠B的和，∠C与∠D的和均为180°，
设四角的度数分别为：4X，6X，2X，8X，由四边形的内角和为360°，
得4X+6X+2X+8X=360°，解得，四角分别为：72°，108°，72°，144°，
同理B中的四角分别为：36°，72°，108°，144°，
同理C中的四角分别为：72°，36°，108°，150°，
同理D中的四角分别为：144°，72°，36°，108°，
所以只有A中的满足∠A与∠B互补，∠C与∠D互补，
故选A．
点评：本题通过设适当的参数，根据四边形的内角和建立方程，求得各角的度数进行判定．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
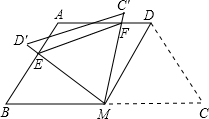如图，等腰梯形ABCD中，AD∥BC，AD=AB=CD=2，∠C=60°，M是BC的中点．
DE．
如图，在梯形ABCD中，AD∥BC，AB=CD，点E在BC的延长线上，且∠BDE=∠ADC．求证：AB•BD=DE•AD．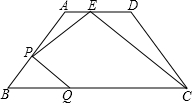
如图，在等腰梯形ABCD中，AD∥BC，AB=5，AD=6，BC=12，点E在AD边上，且AE：ED=1：2，点P是AB边上的一个动点，（P不与A，B重合）过点P作PQ∥CE交BC于点Q，设AP=x，CQ=y，则y与x之间的函数关系是
分别交边CD、BC于点F、E，若AD=3，BC=12，