题目内容
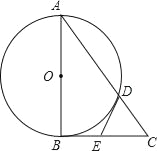
【题目】如图,点![]() 在以
在以![]() 为直径的
为直径的![]() 上,
上,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的平行线交
的平行线交![]() 的延长线于点
的延长线于点![]() .
.
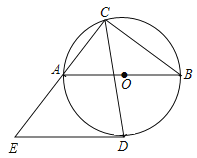
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长度.
的长度.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,由![]() 为
为![]() 的直径得到∠ACB=90
的直径得到∠ACB=90![]() ,根据CD平分∠ACB及圆周角定理得到∠AOD=90
,根据CD平分∠ACB及圆周角定理得到∠AOD=90![]() ,再根据DE∥AB推出OD⊥DE ,即可得到
,再根据DE∥AB推出OD⊥DE ,即可得到![]() 是
是![]() 的切线;
的切线;
(2)过点C作CH⊥AB于H,CD交AB于M,利用勾股定理求出AB,再利用面积法求出CH,求出OH,根据△CHM∽△DOM求出HM得到AM,再利用平行线证明△CAM∽△CED,即可求出DE.
(1)如图,连接OD,
∵![]() 为
为![]() 的直径,
的直径,
∴∠ACB=90![]() ,
,
∵CD平分∠ACB,
∴∠ACD=45![]() ,
,
∴∠AOD=90![]() ,
,
即OD⊥AB,
∵DE∥AB,
∴OD⊥DE ,
∴![]() 是
是![]() 的切线;
的切线;
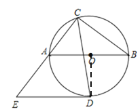
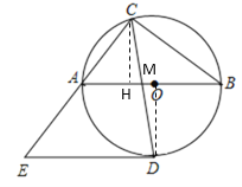
(2)过点C作CH⊥AB于H,CD交AB于M,
∵∠ACB=90![]() ,
,![]() ,
,![]() ,
,
∴AB=![]() ,
,
∵S△ABC=![]() ,
,
∴CH=![]() ,
,
∴AH=![]() ,
,
∴OH=OA-AH=5-3.6=1.4,
∵∠CHM=∠DOM=90![]() ,∠HMC=∠DMO,
,∠HMC=∠DMO,
∴△CHM∽△DOM,
∴![]()
∴![]() =
=![]() ,
,![]() ,
,
∴HM=![]() ,
,
∴AM=AH+HM=![]() ,
,
∵AB∥DE,
∴△CAM∽△CED,
∴![]() ,
,
∴DE=![]() .
.

练习册系列答案
相关题目