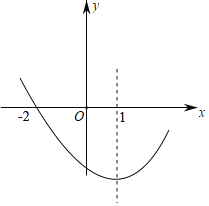
��Ŀ����
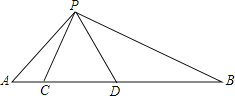
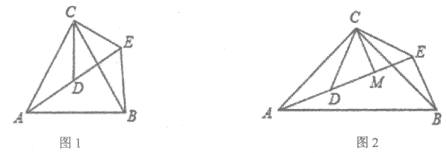
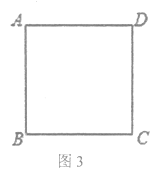
����Ŀ��ͼ1��ʾ������ɡ��ɡ����ֱ��ˮƽ���棬��ʾ��ͼ��ͼ2����ɡ�ս�ʱ����P���A�غϣ���ɡ�����ſ�ʱ������P��A��B�ƶ�������P�����Bʱ��ɡ�ŵ������֪ɡ�ڳſ��Ĺ����У�����PM=PN=CM=CN=6.0���ף�CE=CF=18.0���ף�BC=2.0���ף�
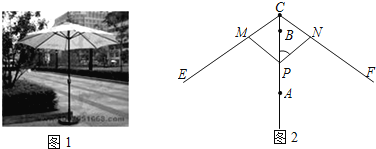
�v1�w��AP����ȡֵ��Χ��
�v2�w�����ⴹֱ�����£�ɡ�ŵ��ʱ����ɡ�µ���Ӱ�v�ٶ�ΪԲ��w���S�v����������w��
���𰸡���1��AP��ȡֵ��Χ�ǣ�0��x��10����2��S���=315����ƽ�����ף���
��������
��1���������⣬��AC=CN+PN����һ�����AB�ij����������AP��ȡֵ��Χ��
��2������MN��EF���ֱ�AC��B��H�������������CMPN���������MB�ij����ٸ������������εĶ�Ӧ�ߵı���ȣ����Բ�İ뾶�������ö��κ���������������ɣ�
��1����BC=2���ף�AC=CN+PN=12���ף�
��AB=AC��BC=10���ף�
����AP=x����AP��ȡֵ��Χ�ǣ�0��x��10��
��2������MN��EF���ֱ�AC��B��H��

��AP=x���ף�
��PM=PN=CM=CN��
���ı���PNCM�����Σ�
��MN��PC���ഹֱƽ�֣�AC�ǡ�ECF��ƽ���ߣ�
PB=![]()
��Rt��MBP�У�PM=6���ף�
��MB2=PM2��PB2=62����6��![]() x��2=6x��
x��2=6x��![]() x2��
x2��
��CE=CF��AC�ǡ�ECF��ƽ���ߣ�
��EH=HF��EF��AC��
�ߡ�ECH=��MCB����EHC=��MBC=90�㣬
���CMB�ס�CEH��
��![]() ��
��
��![]() =��
=��![]() ��2=
��2=![]()
��EH2=9MB2=9��6x��![]() x2����
x2����
��S=��EH2=9����6x��![]() x2����
x2����
��S=��![]() ��x2+54��x��
��x2+54��x��
��x=��![]() =12��0��x��10��
=12��0��x��10��
��x=10ʱ��S���=��![]() ����100+54����10=315����ƽ�����ף���
����100+54����10=315����ƽ�����ף���

 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�