Question

【题目】如图，在Rt△ABC中，∠ACB=90°，AC= ，BC=3，△DEF是边长为a（a为小于3的常数）的等边三角形，将△DEF沿AC方向平移，使点D在线段AC上，DE∥AB，设△DEF与△ABC重叠部分的周长为T．

（1）求证：点E到AC的距离为一个常数；
（2）若AD= ，当a=2时，求T的值；
（3）若点D运动到AC的中点处，请用含a的代数式表示T．

Answer 1

【答案】
（1）

解：由题意得：tanA= = = ，

∴∠A=60°．

∵DE∥AB，

∴∠CDE=∠A=60°．

如答图1所示，过点E作EH⊥AC于点H，

则EH=DEsin∠CDE=a = a．

∴点E到AC的距离为一个常数

（2）

解：若AD= ，当a=2时，如答图2所示．

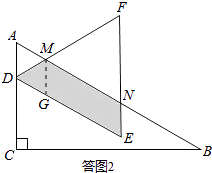
设AB与DF、EF分别交于点M、N．

∵△DEF为等边三角形，∴∠MDE=60°，

由（1）知∠CDE=60°，

∴∠ADM=180°﹣∠MDE﹣∠CDE=60°，

又∵∠A=60°，

∴△ADM为等边三角形，

∴DM=AD= ．

过点M作MG∥AC，交DE于点G，则∠DMG=∠ADM=60°，

∴△DMG为等边三角形，

∴DG=MG=DM= ．

∴GE=DE﹣DG=2﹣ = ．

∵∠MGD=∠E=60°，∴MG∥NE，

又∵DE∥AB，

∴四边形MGEN为平行四边形．

∴NE=MG= ，MN=GE= ．

∴T=DE+DM+MN+NE=2+ + + =

（3）

解：若点D运动到AC的中点处，分情况讨论如下：

①若0＜a≤ ，△DEF在△ABC内部，如答图3所示：

∴T=3a；

②若 ＜a≤ ，点E在△ABC内部，点F在△ABC外部，在如答图4所示：

设AB与DF、EF分别交于点M、N，过点M作MG∥AC交DE于点G．

与（2）同理，可知△ADM、△DMG均为等边三角形，四边形MGEN为平行四边形．

∴DM=DG=NE=AD= ，MN=GE=DE﹣DG=a﹣ ，

∴T=DE+DM+MN+NE=a+ +（a﹣ ）+ =2a+ ；

③若 ＜a＜3，点E、F均在△ABC外部，如答图5所示：

设AB与DF、EF分别交于点M、N，BC与DE、EF分别交于点P、Q．

在Rt△PCD中，CD= ，∠CDP=60°，∠DPC=30°，

∴PC=CDtan60°= × = ．

∵∠EPQ=∠DPC=30°，∠E=60°，∴∠PQE=90°．

由（1）知，点E到AC的距离为 a，∴PQ= a﹣ ．

∴QE=PQtan30°=（ a﹣ ）× = a﹣ ，PE=2QE=a﹣ ．

由②可知，四边形MDEN的周长为2a+ ．

∴T=四边形MDEN的周长﹣PE﹣QE+PQ=（2a+ ）﹣（a﹣ ）﹣（ a﹣ ）+（ a﹣ ）= a+ ﹣ ．

综上所述，若点D运动到AC的中点处，T的关系式为：

T=

【解析】（1）解直角三角形，求得点E到AC的距离等于 a，这是一个定值；（2）如答图2所示，作辅助线，将四边形MDEN分成一个等边三角形和一个平行四边形，求出其周长；（3）可能存在三种情形，需要分类讨论：①若0＜a≤ ，△DEF在△ABC内部，如答图3所示；②若 ＜a≤ ，点E在△ABC内部，点F在△ABC外部，在如答图4所示；③若 ＜a＜3，点E、F均在△ABC外部，如答图5所示．