题目内容
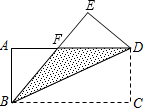如图，沿矩形ABCD的对角线BD折叠，点C落在点E的位置，已知BC=8cm，AB=6cm，那么折叠后的重合部分面积是________cm2．
分析：易得DF=BF，那么可用DF表示出FE，利用直角三角形DFE的三边关系即可求得DF长，然后乘以CD除以2即为阴影部分的面积．
解答：易得AD∥CB，
∴∠ADB=∠DBC，
∵∠FBD=∠DBC
∴∠ADB=∠FBD，
∴DF=BF，
∴FE=8-DF，
∵DE=6，
∴62+（8-DF）2=DF2，
∴DF=
∴S△FBD=
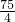．答；三角形FBD的面积
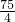cm2．点评：本题通过折叠变换考查学生的逻辑思维能力，解决此类问题，应利用折叠找到相应的直角三角形，利用勾股定理求得所需线段长度．
练习册系列答案
全能测控一本好卷系列答案
相关题目
如图，沿矩形ABCD的对角线BD折叠，点C落在点E的位置，已知BC=8cm，AB=6cm，那么折叠后的重合部分面积是
20、如图，把矩形ABCD沿EF折叠，使点C落在点A处，点D落在点G处，若∠CFE=60°，且DE=2，则边BC的长为
上作正方形PQGH，设AP=x，正方形PQGH和矩形ABCD重合部分的面积为y，回答下列问题：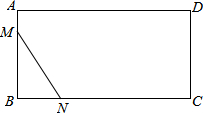
（2010•藤县一模）如图，在矩形ABCD中，AB=10cm，BC=20cm，点M从点A出发沿AB边向点B以1cm/s的速度移动，同时点N从点B出发沿BC边向点C以2cm/s的速度移动（点M、N分别到达B、C两点停止移动）．