题目内容
6.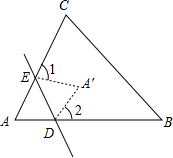 如图,一张△ABC纸片,小明将△ABC沿着DE折叠并压平,点A与A′重合,若∠A=78°,则∠1+∠2=( )
如图,一张△ABC纸片,小明将△ABC沿着DE折叠并压平,点A与A′重合,若∠A=78°,则∠1+∠2=( )| A. | 156° | B. | 204° | C. | 102° | D. | 78° |
分析 先根据图形翻折变化的性质得出△ADE≌△A′DE,∠AED=∠A′ED,∠ADE=∠A′DE,再根据三角形内角和定理求出∠AED+∠ADE及∠A′ED+∠A′DE的度数,然后根据平角的性质即可求出答案.
解答 解:∵△A′DE是△ABC翻折变换而成,
∴∠AED=∠A′ED,∠ADE=∠A′DE,∠A=∠A′=78°,
∴∠AED+∠ADE=∠A′ED+∠A′DE=180°-78°=102°,
∴∠1+∠2=360°-2×102°=156°.
故选A.
点评 本题考查的是图形翻折变换的性质,即折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
16.若关于x的一元二次方程ax2-4x+1=0有两个相等实数根,则a的值是( )
| A. | -1 | B. | 1 | C. | -4 | D. | 4 |
1.慈溪,因治南有溪而得名,慈溪的常住人口约为1460000人,1460000用科学记数法表示为( )
| A. | 0.146×107 | B. | 1.46×105 | C. | 14.6×105 | D. | 1.46×106 |
11.据国家旅游局统计,2017年端午小长假全国各大景点共接待游客约为82600000人次,数据82600000用科学记数法表示为( )
| A. | 0.826×106 | B. | 8.26×107 | C. | 82.6×106 | D. | 8.26×108 |
15. 为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表
(1)求a的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.
 为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).某校九年级50名学生跳高测试成绩的频数表
| 组别(m) | 频数 |
| 1.09~1.19 | 8 |
| 1.19~1.29 | 12 |
| 1.29~1.39 | a |
| 1.39~1.49 | 10 |
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.
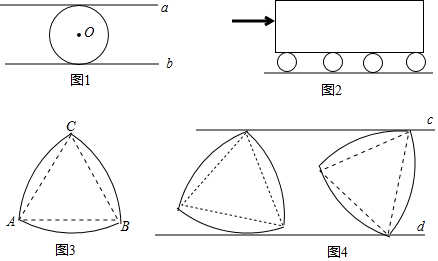
 如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )


