题目内容
如图①，在正方形ABCD中，AB=1，现将△DCA沿DB方向平移到△D′C′A′的位置，且这时点M、N分别是AB、BC的中点，如图②，则阴影部分的周长为________．
2+
分析：根据两个等腰直角△DCA、△D′C′A′的直角边长均为1，将△DCA沿DB方向平移到△D′C′A′的位置，得出线段之间的相等关系，进而得出ME+ED′+D′H+HN+NM，即可得出答案．
解答：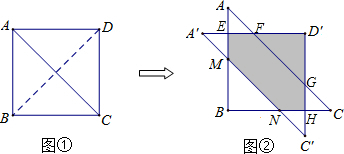
解：∵两个等腰直角△DCA、△D′C′A′的直角边长均为1，将△DCA沿DB方向平移到△D′C′A′的位置，
∴ME=A′E，HN=HC′，AD=A′D′=1，DC=D′C′=1．
∵点M、N分别是AB、BC的中点，∴MN=
AC=，
∴ME+ED′+D′H+HN+NM
=A′E+ED′+D′H+HC′+NM
=A′D′+D′C′+MN
=1+1+
=2+．
故答案为：2+．
点评：此题主要考查了正方形的性质、等腰直角三角形的性质以及平移的性质，根据题意得出ME=A′E，HN=HC′，AD=A′D′=1，DC=D′C′=1是解决问题的关键．
分析：根据两个等腰直角△DCA、△D′C′A′的直角边长均为1，将△DCA沿DB方向平移到△D′C′A′的位置，得出线段之间的相等关系，进而得出ME+ED′+D′H+HN+NM，即可得出答案．
解答：
解：∵两个等腰直角△DCA、△D′C′A′的直角边长均为1，将△DCA沿DB方向平移到△D′C′A′的位置，∴ME=A′E，HN=HC′，AD=A′D′=1，DC=D′C′=1．
∵点M、N分别是AB、BC的中点，∴MN=
AC=，∴ME+ED′+D′H+HN+NM
=A′E+ED′+D′H+HC′+NM
=A′D′+D′C′+MN
=1+1+
=2+
．故答案为：2+
．点评：此题主要考查了正方形的性质、等腰直角三角形的性质以及平移的性质，根据题意得出ME=A′E，HN=HC′，AD=A′D′=1，DC=D′C′=1是解决问题的关键．
练习册系列答案
相关题目
构造一个与上述命题类似的正确命题并加以证明．
26、如图1，在正方形ABCD中，若点E是△DBC内的一点，且DE=DC，BE=CE．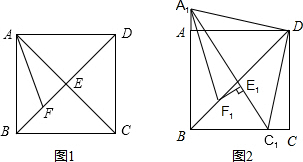
如图1，在正方形ABCD中，对角线AC与BD相交于点E，AF平分∠BAC，交BD于点F．