题目内容
【题目】阅读材料：如图1，在平面直角坐标系中，A、B两点的坐标分别为A（x1 ， y1），B（x2 ， y2），AB中点P的坐标为（xp ， yp）．由xp﹣x1=x2﹣xp ， 得xp= 
，同理yp= 
，所以AB的中点坐标为（ ， ）．由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 ， 所以A、B两点间的距离公式为AB= 
．这两公式对A、B在平面直角坐标系中其它位置也成立．解答下列问题：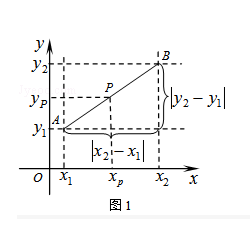
（1）已知M（1，﹣2），N（﹣1，2），直接利用公式填空：MN中点坐标为 ， MN= ．
（2）如图2，直线l：y=2x+2与抛物线y=2x2交于A、B两点，P为AB的中点，过P作x轴的垂线交抛物线于点C．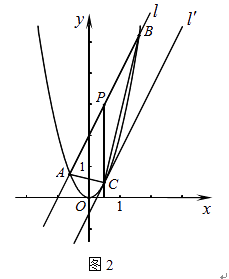
（a）求A、B两点的坐标及C点的坐标；
（b）连结AB、AC，求证△ABC为直角三角形；
（c）将直线l平移到C点时得到直线l′，求两直线l与l′的距离．
【答案】
（1）（0，0）；2 
（2）
解：（a）联立直线、抛物线，得 
，
解得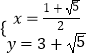 
， 
，
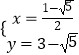即B（ 
，3+ ），A（ 
，3﹣ ）．
由P是AB的中点，得
P（ 
，3）
当x= 时，y=2x2= ，即C点坐标为（ ， ）．
（b）AB2=（ ﹣ ）2+（3+ ﹣3+ ）2=25；
BC2=（ ﹣ ）2+（3+ ﹣ ）2= 
﹣5 ；
AC2=（ ﹣ ）2+（3﹣ ﹣ ）2= +5 ，
∵AC2+BC2=AB2，
∴∠ACB=90°
∴△ABC是直角三角形；
（c）如图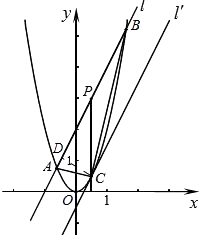 
，
作CD⊥AB于D点，CD 是两直线间的距离，
S△ABC= ABCD= ACBC，
×5CD= 
× 
，
解得CD= 
．
两直线l与l′的距离是
【解析】解：（1）由中点坐标，得 
=0， 
=0，
MN中点坐标为（0，0），
由两点间的距离，得
MN= 
=2 ，
所以答案是：（0，0），2 ．
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点，以及对二次函数的性质的理解，了解增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
