题目内容
【题目】已知![]() 中,记
中,记![]() ,
,![]() .
.
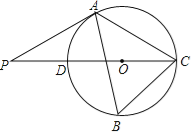
(1)如图![]() ,若
,若![]() 平分
平分![]() ,
,![]() 、
、![]() 分别是
分别是![]() 的外角
的外角![]() 和
和![]() 的平分线,
的平分线,![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的度数,用含
的度数,用含![]() 的代数式表示
的代数式表示![]() 的度数,并说明理由.
的度数,并说明理由.

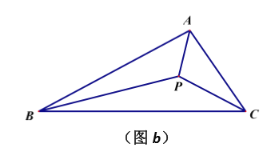
(2)如图![]() ,若点
,若点 ![]() 为
为![]() 的三条内角平分线的交点,
的三条内角平分线的交点,![]() 于点
于点 ![]() , 猜想(1)中的两个结论是否发生变化,补全图形并直接写出你的结论.
, 猜想(1)中的两个结论是否发生变化,补全图形并直接写出你的结论.
![]() .
.
![]() .
.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]()
【解析】
(1)根据三角形内角和定理可求出![]() ,根据邻补角的性质可求出
,根据邻补角的性质可求出![]() ,再根据角平分线的性质可得
,再根据角平分线的性质可得![]() =
=![]() ,根据三角形内角和定理算出∠BPC.由三角形外角的性质得出
,根据三角形内角和定理算出∠BPC.由三角形外角的性质得出![]() ,进而利用直角三角形两锐角互余求出
,进而利用直角三角形两锐角互余求出![]() .
.
(2)根据角平分线性质和三角形外角性质可得![]() ,
,
![]() ,进而可得答案.
,进而可得答案.
(1)解:∵在![]() 中,
中,![]() ,
,![]()

∴![]()
又∵![]() ,
,![]()
∴![]()
∴![]()
∵在![]() 中,
中,![]()
∴![]()
∵![]()
∴![]()
又∵![]() 平分
平分![]()
∴![]()
同理![]()
∵![]()
∴![]()
∴![]()
∵在![]() 中,
中,![]() ,
,![]()
∴![]()
(2)如图2,若点![]() 为
为![]() 的三条内角平分线的交点,
的三条内角平分线的交点,![]() 于点
于点![]() ,猜想(1)中的两个结论已发生变化
,猜想(1)中的两个结论已发生变化

∵点![]() 为
为![]() 的三条内角平分线的交点,
的三条内角平分线的交点,
∴![]() ,
,![]() ,
,
![]() =
=![]() ,即:
,即: ![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
![]() .
.
故答案为:![]() ;
;![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目