Question

（1）观察发现：

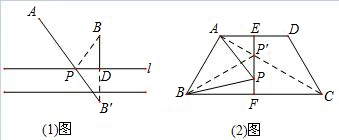
如图1，若点A、B在直线同侧，在直线上求作一点P，使AP+BP最小．

作法：作点B关于直线的对称点B′，连接B′A交直线于点P，点P即为所求．   

如图2，AD是等边△ABC的高，点E是AB的中点，在AD上求作一点P，使BP+PE最小．

作法：连接CE交AD于点P，点P即为所求．若AB=2，则BP+PE的最小值为        ； 

（2）实践运用：

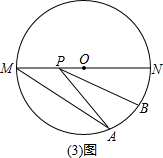
如图3，在正方形ABCD的边长是4，BE=1，在对角线AC上求作一点P，使BP+EP最小，

并求出BP+EP的最小值；

（3）拓展延伸：

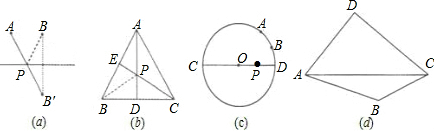
如图4，在四边形ABCD的对角线AC上求作一点P，使∠APB=∠APD．（保留作图痕迹，不必写出作法）

 

Answer 1

解：（1）；

（2）最短距离就等于DE的长度为5；

（3）找B关于AC对称点E，连DE延长交AC于P即可        …………………12分