题目内容
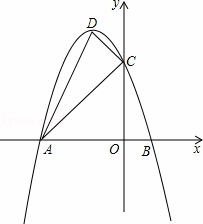
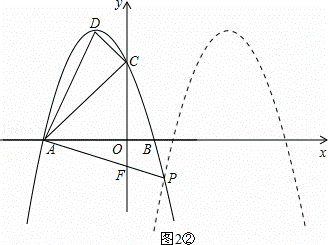
如图,抛物线y=ax2+bx+c的开口向下,与x轴交于点A(﹣3,0)和点B(1,0).与y轴交于点C,顶点为D.
(1)求顶点D的坐标.(用含a的代数式表示);
(2)若△ACD的面积为3.
①求抛物线的解析式;
②将抛物线向右平移,使得平移后的抛物线与原抛物线交于点P,且∠PAB=∠DAC,求平移后抛物线的解析式.
考点:
二次函数综合题.
分析:
(1)已知抛物线与x轴的两交点的横坐标分别是﹣3和1,设抛物线解析式的交点式y=a(x+3)(x﹣1),再配方为顶点式,可确定顶点坐标;
(2)①设AC与抛物线对称轴的交点为E,先运用待定系数法求出直线AC的解析式,求出点E的坐标,即可得到DE的长,然后由S△ACD=![]() ×DE×OA列出方程,解方程求出a的值,即可确定抛物线的解析式;
×DE×OA列出方程,解方程求出a的值,即可确定抛物线的解析式;
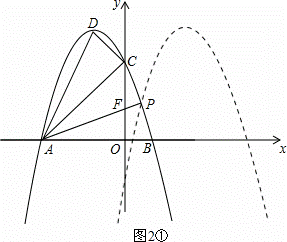
②先运用勾股定理的逆定理判断出在△ACD中∠ACD=90°,利用三角函数求出tan∠DAC=![]() .设y=﹣x2﹣2x+3=﹣(x+1)2+4向右平移后的抛物线解析式为y=﹣(x+m)2+4,两条抛物线交于点P,直线AP与y轴交于点F.根据正切函数的定义求出OF=1.分两种情况进行讨论:(Ⅰ)如图2①,F点的坐标为(0,1),(Ⅱ)如图2②,F点的坐标为(0,﹣1).针对这两种情况,都可以先求出点P的坐标,再得出m的值,进而求出平移后抛物线的解析式.
.设y=﹣x2﹣2x+3=﹣(x+1)2+4向右平移后的抛物线解析式为y=﹣(x+m)2+4,两条抛物线交于点P,直线AP与y轴交于点F.根据正切函数的定义求出OF=1.分两种情况进行讨论:(Ⅰ)如图2①,F点的坐标为(0,1),(Ⅱ)如图2②,F点的坐标为(0,﹣1).针对这两种情况,都可以先求出点P的坐标,再得出m的值,进而求出平移后抛物线的解析式.
解答:
解:(1)∵抛物线y=ax2+bx+c与x轴交于点A(﹣3,0)和点B(1,0),
∴抛物线解析式为y=a(x+3)(x﹣1)=ax2+2ax﹣3a,
∵y=a(x+3)(x﹣1)=a(x2+2x﹣3)=a(x+1)2﹣4a,
∴顶点D的坐标为(﹣1,﹣4a);
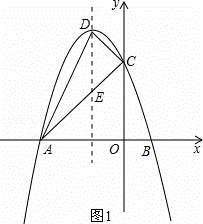
(2)如图1,①设AC与抛物线对称轴的交点为E.
∵抛物线y=ax2+2ax﹣3a与y轴交于点C,
∴C点坐标为(0,﹣3a).
设直线AC的解析式为:y=kx+t,
则:![]() ,
,
解得:![]() ,
,
∴直线AC的解析式为:y=﹣ax﹣3a,
∴点E的坐标为:(﹣1,﹣2a),
∴DE=﹣4a﹣(﹣2a)=﹣2a,
∴S△ACD=S△CDE+S△ADE=![]() ×DE×OA=
×DE×OA=![]() ×(﹣2a)×3=﹣3a,
×(﹣2a)×3=﹣3a,
∴﹣3a=3,解得a=﹣1,
∴抛物线的解析式为y=﹣x2﹣2x+3;
②∵y=﹣x2﹣2x+3,
∴顶点D的坐标为(﹣1,4),C(0,3),
∵A(﹣3,0),
∴AD2=(﹣1+3)2+(4﹣0)2=20,CD2=(﹣1﹣0)2+(4﹣3)2=2,AC2=(0+3)2+(3﹣0)2=18,
∴AD2=CD2+AC2,
∴∠ACD=90°,
∴tan∠DAC=![]() =
=![]() =
=![]() ,
,
∵∠PAB=∠DAC,
∴tan∠PAB=tan∠DAC=![]() .
.
如图2,设y=﹣x2﹣2x+3=﹣(x+1)2+4向右平移后的抛物线解析式为y=﹣(x+m)2+4,两条抛物线交于点P,直线AP与y轴交于点F.
∵tan∠PAB=![]() =
=![]() =
=![]() ,
,
∴OF=1,则F点的坐标为(0,1)或(0,﹣1).
分两种情况:
(Ⅰ)如图2①,当F点的坐标为(0,1)时,易求直线AF的解析式为y=![]() x+1,
x+1,
由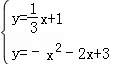 ,解得
,解得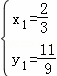 ,
,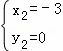 (舍去),
(舍去),
∴P点坐标为(![]() ,
,![]() ),
),
将P点坐标(![]() ,
,![]() )代入y=﹣(x+m)2+4,
)代入y=﹣(x+m)2+4,
得![]() =﹣(
=﹣(![]() +m)2+4,
+m)2+4,
解得m1=﹣![]() ,m2=1(舍去),
,m2=1(舍去),
∴平移后抛物线的解析式为y=﹣(x﹣![]() )2+4;
)2+4;
(Ⅱ)如图2②,当F点的坐标为(0,﹣1)时,易求直线AF的解析式为y=﹣![]() x﹣1,
x﹣1,
由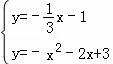 ,解得
,解得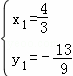 ,
,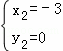 (舍去),
(舍去),
∴P点坐标为(![]() ,﹣
,﹣![]() ),
),
将P点坐标(![]() ,﹣
,﹣![]() )代入y=﹣(x+m)2+4,
)代入y=﹣(x+m)2+4,
得﹣![]() =﹣(
=﹣(![]() +m)2+4,
+m)2+4,
解得m1=﹣![]() ,m2=1(舍去),
,m2=1(舍去),
∴平移后抛物线的解析式为y=﹣(x﹣![]() )2+4;
)2+4;
综上可知,平移后抛物线的解析式为y=﹣(x﹣![]() )2+4或y=﹣(x﹣
)2+4或y=﹣(x﹣![]() )2+4.
)2+4.
点评:
此题是二次函数的综合题,考查了待定系数法求函数的解析式,二次函数的性质,勾股定理的逆定理,三角函数的定义,三角形的面积、两函数交点坐标的求法,函数平移的规律等知识,综合性较强,有一定难度,解题的关键是方程思想、数形结合思想与分类讨论思想的应用.

 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).