Question

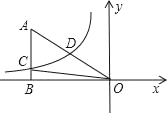
【题目】探索：如图1，在中，，．求证：；

发现：直角三角形中，如果有一个锐角等于，那么这个角所对的直角边等于斜边的_______．

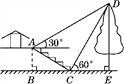
应用：如图2，在中，，，，点从点出发沿方向以秒的速度向点匀速运动，同时点从点出发沿方向以秒的速度向点匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点运动的时间是秒（）．过点作于点，连接，．

（1）四边形能够成为菱形吗？如果能，求出相应的值；如果不能，请说明理由；

（2）当为何值时，为直角三角形？请说明理由．

Answer 1

【答案】探索：；发现：一半；应用：（1）能，当秒时，四边形为菱形；（2）当t=7.5或12秒时，△DEF为直角三角形

【解析】

探索：先判断出BD=AC=AD，进而判断出△ABD是等边三角形，即可得出结论；
发现：直接由发现得出结论；
应用：（1）能．首先证明四边形AEFD为平行四边形，当AE=AD时，四边形AEFD为菱形，即60-4t=2t，解方程即可解决问题；
（2）分三种情形讨论①当∠DEF=90°时，②当∠EDF=90°时．③若∠EFD=90°，分别求解即可．

探索：作边上的中线，

∵在中，，

∴，，

∴是等边三角形

∴；

发现：由探索知，直角三角形中，如果有一个锐角等于30°，那么这个角所对的直角边等于斜边的一半，
故答案为：一半；

应用：（1）能，理由如下：

在中，，，，

∴，

又∵，

∴，

∵，，

∴，

又∵，

∴四边形为平行四边形．

当时，四边形为菱形，即，解得，

∴当秒时，四边形为菱形；

（2）①当时，由（1）知四边形为平行四边形，

∴，

∴．

∵，

∴，

∴，

又，

∴，解得；

②当时，四边形为矩形，

在中，则，

∴，即，

解得；

③若，则与重合，与重合，此种情况不存在．

综上所述，当t=7.5或12秒时，△DEF为直角三角形．