题目内容
对关于x的二次三项式x2+4x+9进行配方得x2+4x+9=（x+m）2+n
（1）求m、n的值；
（2）求x为何值时x2+4x+9有最小值，并且最小值为多少？
（1）求m、n的值；
（2）求x为何值时x2+4x+9有最小值，并且最小值为多少？
分析：（1）将配方后的结果展开后利用各项系数对应相等求得m、n的值即可；
（2）根据求得的m、n的值即可确定成完全平方的形式，然后写出最小值即可．
（2）根据求得的m、n的值即可确定成完全平方的形式，然后写出最小值即可．
解答：解：（1）∵x2+4x+9=（x+m）2+n=x2+2mx+m2+n，
∴2m=4，m2+n=9
解得：m=2，n=5；
（2）∵m=2，n=5，
∴x2+4x+9=（x+m）2+n=（x+2）2+5
∴当x=-2时，有最小值是5．
∴2m=4，m2+n=9
解得：m=2，n=5；
（2）∵m=2，n=5，
∴x2+4x+9=（x+m）2+n=（x+2）2+5
∴当x=-2时，有最小值是5．
点评：本题考查了配方法的应用，由第一题的基础再来解决第二题显得比较简单．
练习册系列答案
走进文言文系列答案
相关题目
1.红用下面的方法对
进行因式分解，请你仿照他的方法分解下面另外三个二次三项式，并把你的解答过程填写在下面的表格中．
| 方程 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 关于x的方程
（ 且 |
|
|
|
、
、
为常数，
）
2.设
是一元二次方程
的两个实根，根据观察表格中的规律，写出二次三项式
的因式分解与之间的关系式。
【小题1】红用下面的方法对
进行因式分解，请你仿照他的方法分解下面另外三个二次三项式，并把你的解答过程填写在下面的表格中．| 方程 |  |  |  因式分解 |
 |  |  |  |
 |  |  |  |
 | | | |
 | | | |
关于x的方程 （  、 、 为常数，且  ） |  |  | |
【小题2】设
是一元二次方程
的两个实根，根据观察表格中的规律，写出二次三项式的因式分解与之间的关系式。
1.红用下面的方法对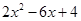
进行因式分解，请你仿照他的方法分解下面另外三个二次三项式，并把你的解答过程填写在下面的表格中．
|
方程 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
关于x的方程
（ 且 |
|
|
|
、
、
为常数，
）
2.设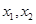
是一元二次方程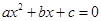
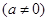的两个实根，根据观察表格中的规律，写出二次三项式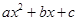
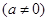的因式分解与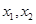之间的关系式。