Question

【题目】如图，分别以的边，所在直线为对称轴作的对称图形和，，线段与相交于点，连接、、、．有如下结论：①；②；③平分；其中正确的结论个数是（ ）

A.0个B.3个C.2个D.1个

Answer 1

【答案】B

【解析】

根据轴对称的性质以及全等三角形的性质对每个结论进行一一判断即可．

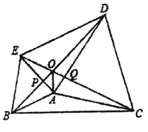
解：∵△ABD和△ACE是△ABC的轴对称图形，
∴∠BAD=∠CAE=∠BAC，AB=AE，AC=AD，
∴∠EAD=3∠BAC360°=3×150°360°=90°，故①正确；
∴∠ABE=∠CAD=×(360°90°150°)=60°，
由翻折的性质得，∠AEC=∠ABD=∠ABC，
又∵∠EPO=∠BPA，
∴∠BOE=∠BAE=60°，故②正确；
在△ACE和△ADB中，

，

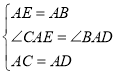∴△ACE≌△ADB，
∴S△ACE=S△ADB，BD=CE，
∴BD边上的高与CE边上的高相等，
即点A到∠BOC两边的距离相等，
∴OA平分∠BOC，故③正确；

综上所述，结论正确的是①②③，
故选：B．