题目内容
已知1+x+x2=0,求代数式1+x+x2+x3+…+x2013的值.
考点:因式分解的应用
专题:
分析:首先分组分解代数式1+x+x2+x3+…+x2013,整体代入得出代数式结果为x2013,再进一步整理1+x+x2=0,得出x2=-x-1,x2+x=-1,由x3=x•x2=x2=x(-x-1)=-(x+x2)=1,代入x2013求得答案即可.
解答:解:∵1+x+x2=0,
∴1+x+x2+x3+…+x2013
=(1+x+x2)+(x3+x4+x5)+…+(x2010+x2011+x2012)+x2013
=x2013;
又∵x2+x=-1,x2=-x-1,
∴x3=x•x2=x2=x(-x-1)=-(x+x2)=1,
∴x2013=(x3)671=1.
∴1+x+x2+x3+…+x2013
=(1+x+x2)+(x3+x4+x5)+…+(x2010+x2011+x2012)+x2013
=x2013;
又∵x2+x=-1,x2=-x-1,
∴x3=x•x2=x2=x(-x-1)=-(x+x2)=1,
∴x2013=(x3)671=1.
点评:此题考查因式分解的运用,分组分解和整体代入是解决问题的关键.

练习册系列答案
相关题目
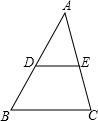 如图,在△ABC中,点D、E分别是AB、AC的中点,则下列结论:
如图,在△ABC中,点D、E分别是AB、AC的中点,则下列结论:(1)BC=2DE,(2)△ADE∽△ABC,(3)
| AD |
| AE |
| AB |
| AC |
| AD |
| CE |
| AE |
| BD |
其中正确的有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
如果|a+2|+(b-1)2=0,那么(a+b)2014的值是( )
| A、-2014 | B、2014 |
| C、-1 | D、1 |
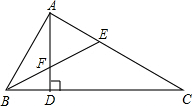 如图所示,∠BAC=90°,AD⊥BC,垂足为D,BE平分∠ABC,交AC于E,交AD于F,试判断△AEF的形状,并说明理由.
如图所示,∠BAC=90°,AD⊥BC,垂足为D,BE平分∠ABC,交AC于E,交AD于F,试判断△AEF的形状,并说明理由.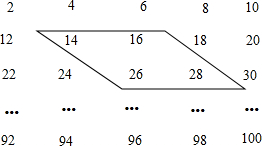 下列数阵是由50个偶数排成的.
下列数阵是由50个偶数排成的. 如图,小林种了一株高40cm的树苗,这株树苗平均每周长高5cm,几周后这株树苗的高超过1米?
如图,小林种了一株高40cm的树苗,这株树苗平均每周长高5cm,几周后这株树苗的高超过1米?