题目内容
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的
直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙0的切线;(2)若DC+DA=6,⊙O的直径为10,求
AB的长度,

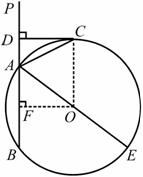 (1)证明:连接OC
(1)证明:连接OC
∵OA=OC
∴![]()
又![]()
∴∠DAC=∠OCA
∴PB∥CO
∴∠PDC=∠DCO=90°
∴OC⊥DC ……3分
又OC为⊙O的半径
∴CD为⊙O的切线. ……4分
(2)解::过O作![]() ,垂足为F,则
,垂足为F,则![]() ,
,
在![]() 中,由勾股定理知
中,由勾股定理知![]()
即![]()
化简得:![]()
解得:![]() 或x=9. ……6分
或x=9. ……6分
由![]() ,知
,知![]() ,故
,故![]() ……7分
……7分
从而AD=2,![]()
因为![]() ,由垂径定理知F为AB的中点,所以
,由垂径定理知F为AB的中点,所以![]() ……8分
……8分
(若设OF=x,可得方程:(x-1)2+x2=25,解得:x1=4,x2=-3(舍去),AF=4-1=3,AB=2AF=6)

练习册系列答案
相关题目
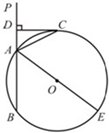 23、如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD丄PA,垂足为D.
23、如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD丄PA,垂足为D.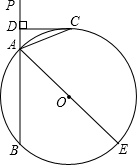 (2012•昌平区一模)如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,C为⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA于D.
(2012•昌平区一模)如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,C为⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA于D. 如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
