题目内容
如图,在直角坐标系中,点A(2,3),点B(-1,1)。

(1)有一小球从点B 水平向右匀速滚去,同时一个机器人从点A以同样的速度直线前进去拦截小球,请你在图中画出机器人最快截住小球的位置点P。(作图要求:尺规作图,保留作图痕迹)
(2)在x轴上找一点Q,使AQ+BQ的值最小,并求出此时点Q的坐标。
(2)在x轴上找一点Q,使AQ+BQ的值最小,并求出此时点Q的坐标。
解:(1)如图:
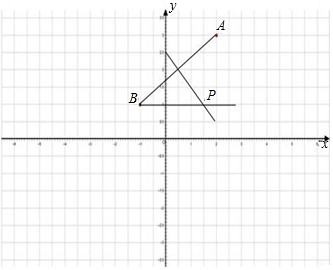 ;
;
(2)作点B关于x轴的对称点B′(-1,-1),连接AB′交x轴于点Q;
设直线AB′的函数关系式为y=kx+b(k≠0),
将A、B′的坐标代入,得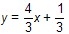
令y=0,得x=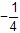
所以点Q的坐标为(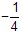 ,0)。
,0)。
 ;
;(2)作点B关于x轴的对称点B′(-1,-1),连接AB′交x轴于点Q;
设直线AB′的函数关系式为y=kx+b(k≠0),
将A、B′的坐标代入,得
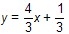
令y=0,得x=
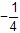
所以点Q的坐标为(
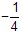 ,0)。
,0)。
练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: