题目内容
 (2012•营口)如图,直线y=-x+b与双曲线y=
(2012•营口)如图,直线y=-x+b与双曲线y=| 1 |
| x |
| 4 |
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
分析:根据直线解析式求出点E、F的坐标,过点O作OM⊥AB于点M,设A(x1,y1)、B(x2,y2),联立两函数解析式求解可得y1=x2,y2=x1,从而判断出点A、B关于OM对称,并求出点A的坐标,然后代入双曲线解析式计算即可得解.
解答: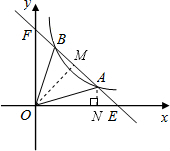 解:令y=0,则-x+b=0,
解:令y=0,则-x+b=0,
解得x=b,
令x=0,则y=b,
所以,点E(b,0)、F(0,b),
所以,OE=OF,
过点O作OM⊥AB于点M,则ME=MF,
设点A(x1,y1)、B(x2,y2),
联立
,
消掉y得,x2-bx+1=0,
根据根与系数的关系,x1•x2=1,
所以y1•y2=1,
所以y1=x2,y2=x1,
所以OA=OB,
所以AM=BM(等腰三角形三线合一),
∵S△AOB=S△OBF+S△OAE,
∴FB=BM=AM=AE,
所以点A(
b,
b),
∵点A在双曲线y=
上,
∴
b×
b=1,
解得b=
.
故答案为:
.
 解:令y=0,则-x+b=0,
解:令y=0,则-x+b=0,解得x=b,
令x=0,则y=b,
所以,点E(b,0)、F(0,b),
所以,OE=OF,
过点O作OM⊥AB于点M,则ME=MF,
设点A(x1,y1)、B(x2,y2),
联立
|
消掉y得,x2-bx+1=0,
根据根与系数的关系,x1•x2=1,
所以y1•y2=1,
所以y1=x2,y2=x1,
所以OA=OB,
所以AM=BM(等腰三角形三线合一),
∵S△AOB=S△OBF+S△OAE,
∴FB=BM=AM=AE,
所以点A(
| 3 |
| 4 |
| 1 |
| 4 |
∵点A在双曲线y=
| 1 |
| x |
∴
| 3 |
| 4 |
| 1 |
| 4 |
解得b=
| 4 |
| 3 |
| 3 |
故答案为:
| 4 |
| 3 |
| 3 |
点评:本题考查了反比例函数与一次函数的交点问题,联立两函数解析式求解得到OA=OB,然后根据三角形的面积求出点A、B、M是线段EF的四等分点,并求出点A的坐标是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
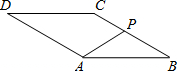 (2012•营口)如图,菱形ABCD的边长为2,∠B=30°.动点P从点B出发,沿B-C-D的路线向点D运动.设△ABP的面积为y(B、P两点重合时,△ABP的面积可以看做0),点P运动的路程为x,则y与x之间函数关系的图象大致为( )
(2012•营口)如图,菱形ABCD的边长为2,∠B=30°.动点P从点B出发,沿B-C-D的路线向点D运动.设△ABP的面积为y(B、P两点重合时,△ABP的面积可以看做0),点P运动的路程为x,则y与x之间函数关系的图象大致为( )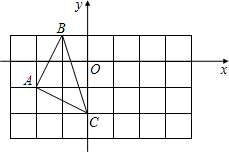 (2012•营口)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1)、B(-1,1)、C(0,-2).
(2012•营口)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1)、B(-1,1)、C(0,-2).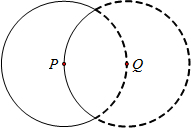 (2012•营口)如图,实线部分为某月牙形公园的轮廓示意图,它可看作是由⊙P上的一段优弧和⊙Q上的一段劣弧围成,⊙P与⊙Q的半径都是2km,点P在⊙Q上.
(2012•营口)如图,实线部分为某月牙形公园的轮廓示意图,它可看作是由⊙P上的一段优弧和⊙Q上的一段劣弧围成,⊙P与⊙Q的半径都是2km,点P在⊙Q上.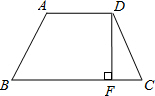 (2012•营口)如图,在等腰梯形ABCD中,AD∥BC,过点D作DF⊥BC于F.若AD=2,BC=4,DF=2,则DC的长为
(2012•营口)如图,在等腰梯形ABCD中,AD∥BC,过点D作DF⊥BC于F.若AD=2,BC=4,DF=2,则DC的长为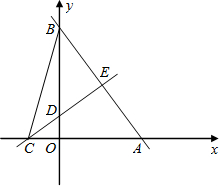 (2012•营口)如图,直线
(2012•营口)如图,直线