题目内容

如图2，已知△ABC是一等腰三角形铁板余料，其中AB=AC=20cm，BC=24cm．若在△ABC上截出一矩形零件DEFG，使EF在BC上，点D、G分别在边AB、AC上．问矩形DEFG的最大面积是多少?

 


过A作AM⊥BC于M，交DG于N，则AM==16cm．设DE=xcm，S矩形=ycm2，则由△ADG∽△ABC，故，即，故DG=(16-x)．

∴y=DG·DE=(16-x)x=-(x2-16x)=-(x-8)2+96，从而当x=8时，y有最大值96．即矩形DEFG的最大面积是96cm2；

练习册系列答案
相关题目
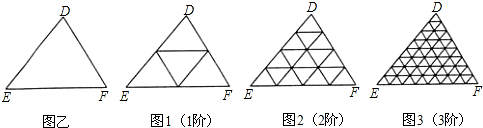
精英家教网定义：若某个图形可分割为若干个都与他相似的图形，则称这个图形是自相似图形．
探究：
（1）如图甲，已知△ABC中∠C=90°，你能把△ABC分割成2个与它自己相似的小直角三角形吗？若能，请在图甲中画出分割线，并说明理由．
（2）一般地，“任意三角形都是自相似图形”，只要顺次连接三角形各边中点，则可将原三分割为四个都与它自己相似的小三角形．我们把△DEF（图乙）第一次顺次连接各边中点所进行的分割，称为1阶分割（如图1）；把1阶分割得出的4个三角形再分别顺次连接它的各边中点所进行的分割，称为2阶分割（如图2）…依次规则操作下去．n阶分割后得到的每一个小三角形都是全等三角形（n为正整数），设此时小三角形的面积为SN．
①若△DEF的面积为10000，当n为何值时，2＜Sn＜3？（请用计算器进行探索，要求至少写出三次的尝试估算过程）
②当n＞1时，请写出一个反映Sn-1，Sn，Sn+1之间关系的等式．（不必证明）精英家教网
精英家教网如图，若已知△ABC中，D、E分别为AB、AC的中点，则可得DE∥BC，且DE=
12
BC．根据上面的结论：
（1）你能否说出顺次连接任意四边形各边中点，可得到一个什么特殊四边形并说明理由；
（2）如果将（1）中的“任意四边形”改为条件是“平行四边形”或“菱形”或“矩形”或“等腰梯形”，那么它们的结论又分别怎样呢？请说明理由．
（2013•德州）（1）如图1，已知△ABC，以AB、AC为边向△ABC外作等边△ABD和等边△ACE，连接BE，CD，请你完成图形，并证明：BE=CD；（尺规作图，不写作法，保留作图痕迹）；
（2）如图2，已知△ABC，以AB、AC为边向外作正方形ABFD和正方形ACGE，连接BE，CD，BE与CD有什么数量关系？简单说明理由；
（3）运用（1）、（2）解答中所积累的经验和知识，完成下题：
如图3，要测量池塘两岸相对的两点B，E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=100米，AC=AE，求BE的长．
（1）添线补全如图1几何体的三视图．

（2）如图2，已知△ABC．请你确定一点P，使PB=PC，且点P到∠B的两边距离相等．
如图1，已知△ABC中，AB=BC=1，∠ABC=90°，把一块含30°角的直角三角板DEF的直角顶点D放在AC的中点上（直角三角板的短直角边为DE，长直角边为DF），将直角三角板DEF绕D点按逆时针方向旋转．
（1）在图1中，DE交边AB于M，DF交边BC于N
①证明：DM=DN
②在这一旋转过程中，直角三角板DEF与△ABC的重叠部分为四边形DMBN，请说明四边形DMBN的面积是否发生变化？若发生变化，请说明是如何变化的？若不发生变化，求出其面积
（2）继续旋转至如图2的位置，延长AB交DE于M，延长BC交DF于N，DM=DN是否仍然成立？若成立，请给出证明；若不成立，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网